// google adsence用 電験３種過去問【2021年理論 問16】 | 電気主任技術者のいろは

電験３種過去問【2021年理論 問16】

2022年11月26日

【電気計測】測定計器による電力損失と誤差率《計算問題》

　図のように、電源E[V]、負荷抵抗R[Ω]、内部抵抗Rv[Ω]の電圧計及び内部抵抗Ra[Ω]の電流計を接続した回路がある。この回路において、電圧計及び電流計の指示値がそれぞれV1[V]、I1[A]であるとき、次の(a)及び(b)の問に答えよ。ただし、電圧計と電流計の指示値の積を負荷抵抗R[Ω]の消費電力の測定値とする。

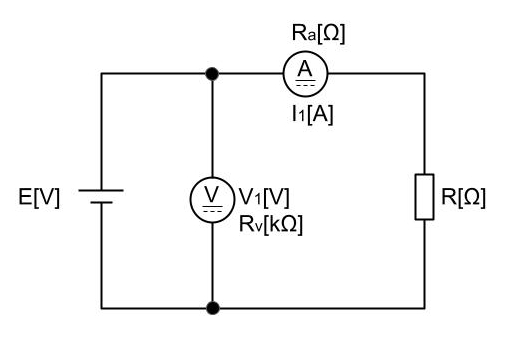
 （a）電流計の電力損失の値[W]を表す式として、正しいものを次の（１）～（５）のうちから一つ選べ。

（１）\(\displaystyle \frac{V_1^2}{R_a}\)

（２）\(\displaystyle \frac{V_1^2}{R_a}-I_1^2R_a\)

（３）\(\displaystyle \frac{V_1^2}{R_v}-I_1^2R_a\)

（４）\(\displaystyle I_1^2R_a\)

（５）\(\displaystyle I_1^2R_a-I_1^2R_v\)

（b）今、負荷抵抗R=320Ω、電流計の内部抵抗Ra=4Ωが分かっている。
　この回路で得られた負荷抵抗R[Ω]の消費電力の測定値V1I1[W]に対して、R[Ω]の消費電力を真値とするとき誤差率の値[％]として、最も近いものを次の（１）～（５）のうちから一つ選べ。

（１）0.3
（２）0.8
（３）0.9
（４）1.0
（５）1.2

解答と解説はこちら

解答

（a）：（４）
（b）：（５）

解説

（a）内部抵抗Ra[Ω]の電流計が消費する電力Pa[W]は、電流計の指示値がI1[A]であるので

\(\displaystyle P_a=I_1^2R_a\text{[W]}\)

（b）R[Ω]での消費電力の真値PR[W]は、

\(\displaystyle P_R=I_1^2R\text{[W]}\)

負荷抵抗R[Ω]の消費電力の測定値V1I1[W]は

\(\displaystyle V_1I_1=(I_1R_a+I_1R)I_1=I_1^2(R_a+R)\text{[W]}\)

このとき、誤差率ε[％]は

\(\displaystyle ε=\frac{V_1I_1-P_R}{P_R}\times100\)

\(\displaystyle =\frac{I_1^2(R_a+R)-I_1^2R}{I_1^2R}\times100\)

\(\displaystyle =\frac{(R_a+R)-R}{R}\times100\)

\(\displaystyle =\frac{R_a}{R}\times100\)

\(\displaystyle =\frac{4}{320}\times100=1.2\text{[%]}\)

<<前問　　次問>>

 

電験３種過去問理論過去問, 電験3種, 理論, 電気計測, 2021年

Posted by ちゅん