電験３種過去問【2018年理論 問1】
【電磁気】帯電導体球に働く力《計算問題》
次の文章は、帯電した導体球に関する記述である。
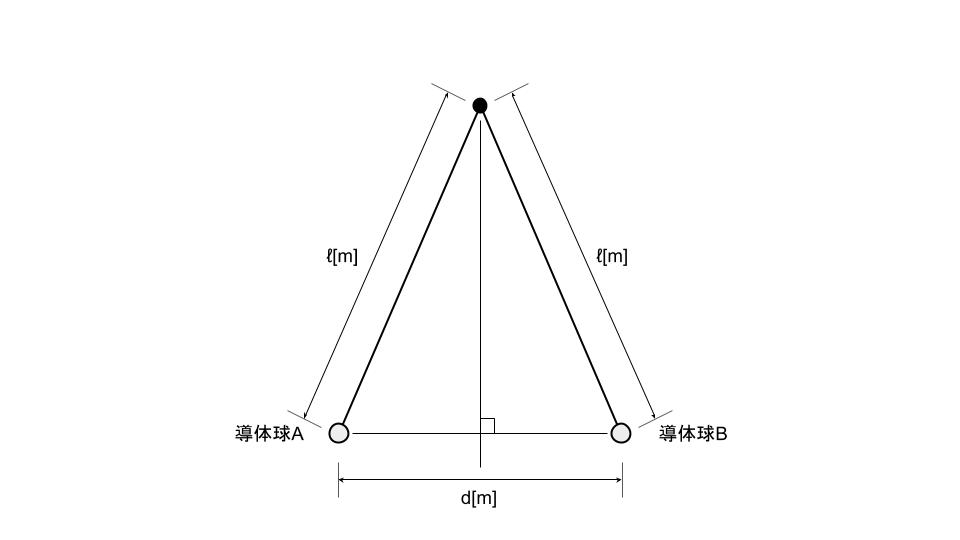
真空中で導体球A及びBが軽い絶縁体の糸で固定点Oからつり下げられている。真空の誘電率をε0[F/m]、重力加速度をｇ[ｍ/s2]とする。A及びBは同じ大きさと質量ｍ[kg]をもつ。糸の長さは各導体球の中心点が点Oから距離ｌ[ｍ]となる長さである。
まず、導体球A及びBにそれぞれ電荷Q[C]、３Q[C]を与えて帯電させたところ、静電力による【（ア）】が生じ、図のようにA及びBの中心点間がｄ[ｍ]離れた状態で釣り合った。ただし、導体球の直径はｄに比べて十分に小さいとする。このとき、個々の導体球において、静電力F＝【（イ）】[N]、重力ｍｇ[N]、糸の張力T[N]、の三つの力が釣り合っている。三平方の定理よりF2+(mg)2=T2が成り立ち、張力の方向を考えるとF/Tはd/(2l)に等しい、これらよりTを消去し整理すると、ｄが満たす式として、
k{d/(2l)}3=√[1-{d/(2l)}2]が導かれる。ただし、係数ｋ＝【（ウ）】である。
次に、AとBとを一旦接触させたところAB間で電荷が移動し、同電位となった。そしてAとBとが力の釣合いの位置に戻った。接触前に比べ、距離ｄは【（エ）】した。
上記の記述中の空白個所（ア）、（イ）、（ウ）及び（エ）に当てはまる組合せとして、正しいものを次の（１）～（５）のうちから一つ選べ。
| （ア） | （イ） | （ウ） | （エ） | |
| （１） | 反発力 | 3Q2/(4πε0d2) | 16πε0l2mg/(3Q2) | 増加 |
| （２） | 吸引力 | Q2/(4πε0d2) | 4πε0l2mg/(Q2) | 増加 |
| （３） | 反発力 | 3Q2/(4πε0d2) | 4πε0l2mg/(Q2) | 増加 |
| （４） | 反発力 | Q2/(4πε0d2) | 16πε0l2mg/(3Q2) | 減少 |
| （５） | 吸引力 | Q2/(4πε0d2) | 4πε0l2mg/(Q2) | 減少 |
https://archivelog.net/denken3-kakomon/
https://archivelog.net/denken/