解答
（1）が正しい。
解説
周波数伝達関数
入力信号が正弦波交流である場合、定常状態での出力信号\(\displaystyle \dot{E}_o(jω)\)と入力信号\(\displaystyle \dot{E}_i(jω)\)の比は、入力信号の角周波数ωの関数となる。これを周波数伝達関数G(jω)と呼ぶ。
\(\displaystyle G(jω)=\frac{\dot{E}_o(jω)}{\dot{E}_i(jω)}\)
RL直列回路の過渡現象
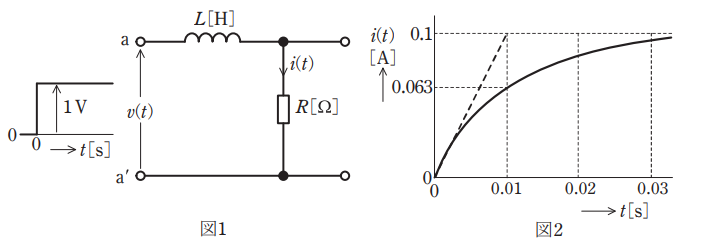
開放電圧がV[V]で出力抵抗が十分に低い直流電圧源と、インダクタンスがL[H]のコイルが与えられ、抵抗R[Ω]がスイッチSを介して直列接続されている。時刻t＝0でスイッチSを閉じ、コイルの電流iL[A]の時間に対する変化を計測して、波形として表す。
RL直列回路へ、時刻t=0[s]から、直流電源V[V]を与えるとき回路に流れる電流i(t)[A]は、
\(\displaystyle i(t)=\frac{V}{R}(1-e^{-\frac{R}{L}t})\text{[A]}\)
過渡電流の時間変化の指標となる時定数τは、指数(e)係数の逆数であるので
\(\displaystyle τ=\frac{L}{R}\text{[s]}\)
過渡電流の時定数は、最終電流\(\displaystyle I=\frac{V}{R}\text{[A]}\)の\(\displaystyle (1-e^{-1})≒0.632\)倍すなわち63.2[％]となる時間である。
電気回路の学習帳
RL直列回路に流れる過渡電流は、
\(\displaystyle i(t)=\frac{V}{R}(1-e^{-\frac{R}{L}t})\text{[A]}\)となる。
最終電流\(\displaystyle I=\frac{V}{R}\text{[A]}\)は、図２より 0.1 A となり、また V = 1 [V] であるので、
\(\displaystyle I=\frac{V}{R}=\frac{1}{R}=0.1\)
∴\(\displaystyle R=10\)[Ω]
過渡電流の時定数τは、
\(\displaystyle τ=\frac{L}{R}\text{[s]}\)で与えられ、図２より 0.01 s であるので、
\(\displaystyle τ=\frac{L}{R}=\frac{L}{10}=0.01\)
∴\(\displaystyle L=0.1\)[H]
周波数伝達関数G(jω)は、題意より入力は端子電圧、出力は抵抗に流れる電流であるので
\(\displaystyle G(jω)=\frac{\dot{E}_o(jω)}{\dot{E}_i(jω)}\)
\(\displaystyle =\frac{i(t)}{V}\)
\(\displaystyle =\frac{\frac{V}{R+jωL}}{V}\)
\(\displaystyle =\frac{1}{R+jωL}\)
\(\displaystyle =\frac{1}{10+jω0.1}\)
\(\displaystyle =\frac{0.1}{1+jω0.01}\)
