解答
（a）:（5）が正しい。
（b）:（2）が正しい。
解説
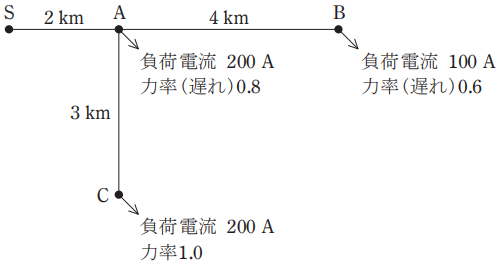
(a) S-A 間を流れる電流の値[ A ]を求める。
A 点の負荷に流れる電流は
IA = 200(0.8 – j0.6)
= 160 – j120 [A]
B 点の負荷に流れる電流は
IB = 100(0.6 – j0.8)
= 60 – j80 [A]
C 点の負荷に流れる電流は
IC = 200 [A]
S-A 間を流れる電流は
IS = IA + IB +IC
= 420 – j200 [A]
|IS|=\(\sqrt{420^2+200^2}\)=465.2[A]
(b) A-B における電圧降下率の値 [ % ] を求める。
電圧降下率
線路の電圧降下の度合いを示す、電圧降下率εは、電圧降下を受電端電圧(相電圧)に対する百分率で表す。
\(\displaystyle ε=\frac{E_s-E_r}{E_r}\times 100=\frac{ILS}{E_r}\times 100\) [%]
A-B における１線当たり電圧降下（相電圧）は
EAB = IB × 4 (0.3 + j0.3)
= (60 – j80)(1.2 + j1.2)
= 168 – j24[V]
\(|E_{AB}|=\sqrt{168^2+24^2}=169.7\)[A]
S-A における１線当たり電圧降下（相電圧）は
ESA = IS × 2 (0.3 + j0.3)
= (420 – j200)(0.6 + j0.6)
= 372 + j132[V]
B 点の受電端電圧（相電圧）は、送電端線間電圧が 6 600 V (相電圧は6 600/√3 V)であるので
\(\displaystyle E_B=\frac{6600}{\sqrt3}-E_{SA}-E_{AB}\\
=3810.5-(336+j48)-(168-j24)\\
=3306.5-j24[V]\\
|E_B|=\sqrt{3306.5^2+24^2}=3306.6[V]\)
A-B における電圧降下率εは、
\(\displaystyle ε=\frac{E_{AB}}{E_B}\times 100\\
\displaystyle =\frac{169.7}{3306.6}\times 100\\
=5.13[％]\)
追加学習は配電の学習帳で
