// google adsence用 電験３種過去問【2014年電力 問15】 | 電気主任技術者のいろは

電験３種過去問【2014年電力 問15】

2022年4月24日

【水力発電】位置水頭と水車出力に関する計算《計算問題》

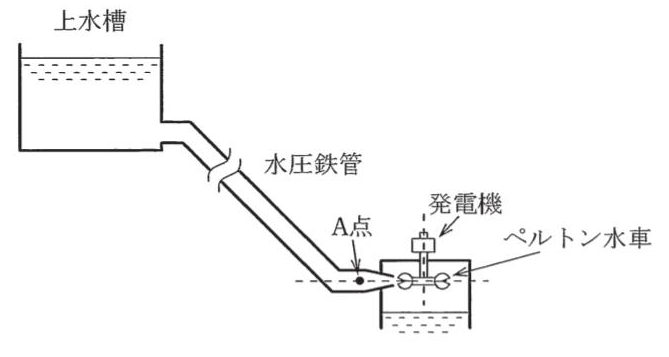
　ぺルトン水車を１台もつ水力発電所がある。図に示すように、水車の中心線上に位置する鉄管のA点において圧力ｐ[Pa]と流速ｖ[m/s]を測ったところ、それぞれ3000kPa、5.3m/sの値を得た。また、このＡ点の鉄管断面は内径1.2ｍの円である。次の(a)及び(b)の問に答えよ。
　ただし、Ａ点における全水頭Ｈ[m]は位置水頭、圧力水頭、速度水頭の総和として\(\displaystyle h+\frac{p}{ρg}+\frac{v^2}{2g}\)より計算できるが、位置水頭hはA点が水車中心線上に位置することから無視できるものとする。また、重力加速度はg=9.8m/s2、水の密度はρ=1000kg/m3とする。

（a）ペルトン水車の流量の値[m3/s]として、最も近いものを次の（１）～（５）のうちから一つ選べ。

(1) 3　　(2) 4　　(3) 5　　(4) 6　　(5) 7 

（b）水車出力の値[kW]として、最も近いものを次の（１）～（５）のうちから一つ選べ。
　ただし、A点から水車までの水路損失は無視できるものとし、また水車効率は88.5％とする。

(1) 13000　　(2) 14000　　(3) 15000　　(4) 16000　　(5) 17000 

解答と解説はこちら

解答

（a）（４）
（b）（４）

解説

（a）流体力学の連続の定理より、Q＝Av（流量Q[m3/s]、断面積A[m2]、流体の速度v[m/s]）となるので、A点の流量は
　\(\displaystyle Q=Av=\pi r^2v=\pi\times0.6^2\times5.3=6.0[m^3/s]\)

（b）有効落差H[m]は、ベルヌーイの定理から、
　\(\displaystyle H=h+\frac{p}{ρg}+\frac{v^2}{2g}=0+\frac{3000\times10^3}{1000\times9.8}+\frac{5.3^2}{2\times9.8}=307.6[m]\)

　水車出力Pは、水車効率をηとすると
　\(\displaystyle P=9.8QHη＝9.8\times6.0\times307.6\times0.885≒16000[kW]\)

<<前問　　次問>>

 

電験３種過去問電力過去問, 電験3種, 電力, 水力発電, 2014年

Posted by ちゅん