電験３種過去問【2013年電力 問9】
【送電】架線の水平張力に関する計算《計算問題》
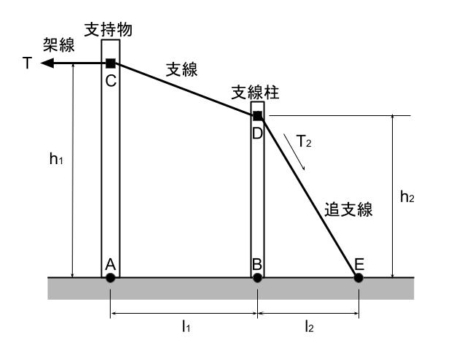
図のように、架線の水平張力T[N]を支線と追支線で、支持物と支線柱を介して受けている。支持物の固定点Cの高さをh1[m]、支線柱の固定点Dの高さをh2[m]とする。また、支持物と支線柱間の距離ABをl1[m]、支線柱と追支線地上固定点Eとの根開きBEをl2[m]とする。
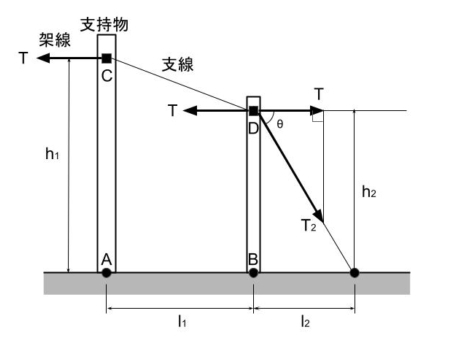
支持物及び支線柱が受ける水平方向の力は、それぞれ平行しているという条件で、追支線にかかる張力T2[N]を表した式として、正しいものを次の（１）～（５）のうちから一つ選べ。
ただし、支線、追支線の自重及び提示していない条件は無視する。
（１）\displaystyle\frac{T\sqrt{h_2^2+l_2^2}}{l_2}
（２）\displaystyle\frac{Tl_2}{\sqrt{h_2^2+l_2^2}}
（３）\displaystyle\frac{T\sqrt{h_2^2+l_2^2}}{\sqrt{(h_1-h_2)^2+l_1^2}}
（４）\displaystyle\frac{T\sqrt{(h_1-h_2)^2+l_1^2}}{\sqrt{h_2^2+l_2^2}}
（５）\displaystyle\frac{Th_2\sqrt{(h_1-h_2)^2+l_1^2}}{(h_1-h_2)\sqrt{h_2^2+l_2^2}}
解答
（１）
解説
架線に掛かる水平張力T[N]の、水平成分はD点においても等しい。D点において追支線に掛かる張力T2[N]は下図のようなベクトル成分となる。
追支線と水平面がなす角をθ[°]とすると、
\displaystyle T=T_2cosθ
ここで、上図より三平方の定理を用いれば
\displaystyle cosθ=\frac{l_2}{\sqrt{h_2^2+l_2^2}}
が成り立つ。したがって、
\displaystyle T_2=\frac{T}{cosθ}=\frac{T\sqrt{h_2^2+l_2^2}}{l_2}
https://archivelog.net/denken3-kakomon/
https://archivelog.net/denken/