電験２種過去問【2021年理論 問3】

解答

(１)：（ホ）
(２)：（チ）
(３)：（ワ）
(４)：（ト）
(５)：（ニ）

解説

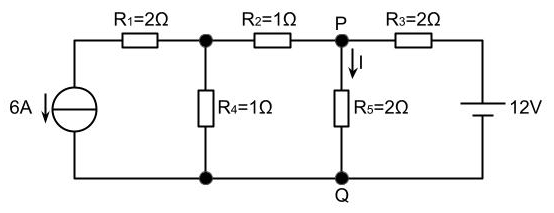
　図の直流回路において、重ね合わせの理を用いて抵抗R₅を流れる電流Iについて解析する。ただし、抵抗R₅に流れる電流の正方向を図中の節点PからQの向きとする。
　重ね合わせの理は、\(\fbox{線形}\)回路において成立する定理である。図の回路において、電圧源を残して電流源を取り除いた回路を考え（このとき、電流源は\(\fbox{開放}\)除去されている）、抵抗R₅に流れる電流I_aを求める。

電流源を取り除いた後の、電圧源からみたPQ間の合成抵抗は、

\(\displaystyle R_{245}=(R_2+R_4)//R_5= \frac{(R_2+R_4)R_5}{(R_2+R_4)+R_5}=\frac{4}{4}=1\text{[Ω]}\)

電圧源の電圧をV[V]としたとき、PQ間の電圧は、

\(\displaystyle V_{PQ}=V\times\frac{R_{245}}{R_{245}+R_3}=V\times\frac{1}{3}=4\text{[V]}\)…（１）

\(\displaystyle I_{a}=\frac{V_{PQ}}{R_5}=\frac{4}{2}=2\text{[A]}\)…（２）

I_a＝\(\fbox{2}\)Aとなる。

　次に、図の回路において、電流源を残して電圧源を取り除いた回路を考え（このとき電圧源は短絡除去されている）、抵抗R₅に流れる電流I_bを求める。

\(\displaystyle R_2\),\(\displaystyle R_3\),\(\displaystyle R_5\)の合成抵抗は

\(\displaystyle R_{235}=R_2+(R_3//R_5)= 1+1=2\text{[Ω]}\)

電流の分流則により、\(\displaystyle R_{235}\)に流れる電流は

\(\displaystyle I_{235}=-6\times\frac{R_4}{R_{235}+R_4}=-6\times\frac{1}{3}=-2\text{[A]}\)

PQ間に流れる電流\(\displaystyle I_{b}\)は、\(\displaystyle I_{235}\)に流れる電流の半分であるので

\(\displaystyle I_{b}=\frac{ I_{235}}{2}=-1\text{[A]}\)

電流I_aとI_bを重ね合わせれば、抵抗R₅に流れる電流は

\(\displaystyle I＝I_a+I_b=2-1=1\text{[A]}\)

つまりI＝\(\fbox{1}\)Aと求められる。

　また、図の回路において、電圧源の電圧Vを調整して、抵抗R₅に流れる電流がI＝0Aとなるには、\(\displaystyle I_a=1\text{[A]}\)となるときなので、

式（１）、式（２）より

\(\displaystyle I_{a}=\frac{V\times\frac{1}{3}}{R_5}=\frac{V}{6}=1\text{[A]}\)

つまり、電圧源の電圧を\(\fbox{6}\)Vとすればよい。