// google adsence用 電験２種過去問【2021年理論 問2】 | 電気主任技術者のいろは

電験２種過去問【2021年理論 問2】

2022年4月24日

【電磁気】強磁性体の磁気特性（ヒステリシスループ）《空所問題》

　次の文章は、強磁性体の磁気特性に関する記述である。文中の\(\fbox{空所欄}\)に当てはまる最も適切なものを解答群の中から選べ。なお、ここでは、強磁性体に流れる渦電流は無視する。
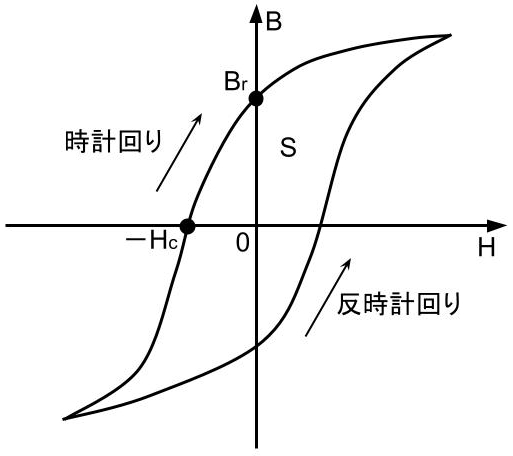
　強磁性体に一様な交番磁界を印加すると、強磁性体内の磁束密度B[T]は磁界H[A/m]に比例せず、定常状態において図に示すような\(\fbox{（１）}\)の軌跡を描く。これをヒステリシスループと呼ぶ。図中のBr[T]とHc[A/m]は、それぞれ\(\fbox{（２）}\)と保磁力と呼ばれる。強磁性体を永久磁石として用いる場合、\(\fbox{（３）}\)材料が望ましい。
　この特性により生じる損失をヒステリシス損と呼び、それは印加する交番磁界の\(\fbox{（４）}\)に比例する。ヒステリシスループで囲まれた部分の面積S[J/m3]は、交番磁界1周期における強磁性体内で消費される単位体積当たりのエネルギーを表す。ここで、体積1.5×10-3ｍ3の強磁性体に60Hzの一様な交番磁界を与えたところ、S=5.0×102J/m3であったとする。このときのヒステリシス損は\(\fbox{（５）}\)Wである。

［問２の解答群］

(ｲ)\(\displaystyle \text{減磁力}\)　(ﾛ)\(\displaystyle \text{時計回り}\)　(ﾊ)\(\displaystyle \text{反時計周り}\)

(ﾆ)\(\displaystyle B_r\text{が大きく}H_c\text{が小さい}\)　(ﾎ)\(\displaystyle90\)　(ﾍ)\(\displaystyle \text{周波数の2乗}\)

(ﾄ)\( \displaystyle \text{最大磁束密度}\)　(ﾁ)\( \displaystyle\text{周波数}\)　(ﾘ)\( \displaystyle 6\)

(ﾇ)\(\displaystyle B_r\text{と}H_c\text{の両方が大きい}\)　(ﾙ)\( \displaystyle 0.75\)　(ｦ)\( \displaystyle \text{周波数の1.6乗}\)

(ﾜ)\(\displaystyle B_r\text{が小さく}H_c\text{が大きい}\)　(ｶ)\( \displaystyle 45\)　(ﾖ)\( \displaystyle 残留磁束密度\)

解答と解説はこちら

解答

(１)：（ハ）
(２)：（ヨ）
(３)：（ヌ）
(４)：（チ）
(５)：（カ）

解説

　強磁性体に一様な交番磁界を印加すると、強磁性体内の磁束密度B[T]は磁界H[A/m]に比例せず、定常状態において図に示すような\(\fbox{時計回り}\)の軌跡を描く。これをヒステリシスループと呼ぶ。図中のBr[T]とHc[A/m]は、それぞれ\(\fbox{残留磁束密度}\)と保磁力と呼ばれる。強磁性体を永久磁石として用いる場合、\(\fbox{Br[T]とHc[A/m]の両方が大きい}\)材料が望ましい。
　この特性により生じる損失をヒステリシス損と呼び、それは印加する交番磁界の\(\fbox{周波数}\)に比例する。ヒステリシスループで囲まれた部分の面積S[J/m3]は、交番磁界1周期における強磁性体内で消費される単位体積当たりのエネルギーを表す。ここで、体積1.5×10-3ｍ3の強磁性体に60Hzの一様な交番磁界を与えたところ、S=5.0×102J/m3であったとする。このときのヒステリシス損は\(\fbox{45}\)Wである。

（５）全体積における交番磁界1周期のヒステリシス損Wh[J]は

\(\displaystyle W_h=1.5\times10^{-3}\times5.0\times10^2=0.75\text{[J]}\)

60Hzにおけるヒステリシス損Ph[W]は、1秒間に交番磁界60周期であるため

\(\displaystyle P_h=0.75\times60=45\text{[J/s]}=45\text{[W]}\)

<<前問　　次問>>

 

電験２種過去問理論過去問, 電験2種, 理論, 電磁気, 2021年

Posted by ちゅん