電験2種過去問【2019年理論 問5】
【電磁気】無限長導体に流れる電流が作る磁界《空所問題》
次の文章は、電流が作る磁界に関する記述である。文中の\(\fbox{空所欄}\)に当てはまる最も適切なものを解答群の中から選べ。
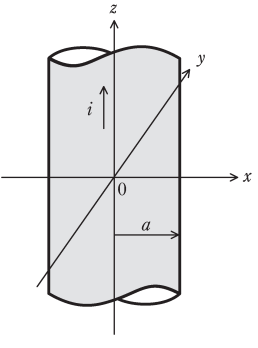
x、y、z軸の直交座標系で表される真空中に、図のようにz軸を中心軸とした半径aの無限長円柱導体が存在している。導体中にはz軸の正の方向に電流が流れており、電流密度i(>0)は場所によらず一定とする。なお、導体の透磁率は真空と同じ\(\mu_0\)とする。
z軸を中心とした半径\(r=\sqrt{x^2+y^2}\)の円断面中を流れる電流は、導体内部(r≦a)では\(\fbox{(1)}\) となるので、アンペアの周回積分の法則を用いてz軸から距離rの地点における磁束密度の大きさを求めることができる。導体内部(r≦a)の磁束密度の大きさ\(B_{in}\)は、
\(B_{in}=\fbox{(2)}\)
導体外部の真空中(r>a)の磁束密度の大きさ\(B_{out}\)は、
\(B_{out}=\fbox{(3)}\)
となるので、磁束密度の大きさはr=aにおいて、最大値
\(B_{max}=\fbox{(4)}\)
をとる。磁界は電流を取り巻くようにできることを考慮すると、磁束密度のy方向成分\(B_y\)のx軸に沿った分布の概形は\(\fbox{(5)}\)のようになる。
[問5の解答群]
\(\small{\begin{array}{ccc}
(イ)&\displaystyle\frac{\mu_0ri}{2}&(ロ)&\displaystyle\frac{\mu_0r^3i}{2a}&(ハ)&\displaystyle\frac{\mu_0i}{2a}\\
(ニ)&\displaystyle\frac{\mu_0a^2i}{2r}&(ホ)&2\pi ri&(ヘ)&\displaystyle\frac{\mu_0i}{2r}\\
(ト)&\pi r^2i&(チ)&\displaystyle\frac{\mu_0ri}{2a^2}&(リ)&\displaystyle\frac{\pi r^3i}{4}\\
(ヌ)&\displaystyle\frac{\mu_0ai}{2}&(ル)&\displaystyle\frac{\mu_0r^2i}{2}&(ヲ)&\displaystyle\frac{\mu_0a^2i}{2}\\
\end{array}}\)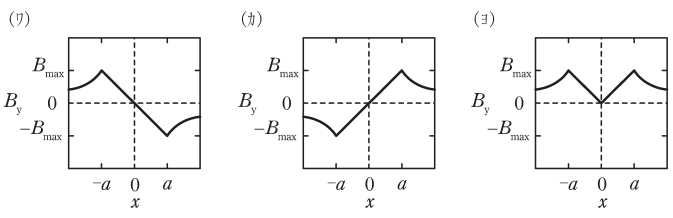


ディスカッション
コメント一覧
まだ、コメントがありません