電験３種過去問【2020年機械 問9】

解答 

（２）

解説

　二次線間電圧6.6ｋVの二次巻線に8000ｋV・Aの誘導性負荷が接続されているとき、流れる二次電流I₂＝8000/(√3×6.6)＝700Aとなる。一次線間電圧と二次線間電圧の変圧比V₁/V₂＝66/6.6＝10であるので、二次電流I₂による一次線電流をI₁₂とすると、V₁/V₂＝I₂/I₁₂であるから、I₁₂＝I₂×V₂/V₁＝700×1/10＝70Aとなる。

　三次線間電圧3.3ｋVの二次巻線に4800ｋV・Aのコンデンサが接続されているとき、流れる三次電流I₃＝4800/(√3×3.3)＝840Aとなる。一次線間電圧と三次線間電圧の変圧比V₁/V₃＝66/3.3＝20であるので、三次電流I₃による一次線電流をI₁₃とすると、V₁/V₃＝I₃/I₁₃であるから、I₁₃＝I₃×V₃/V₁＝840×1/20＝42Aとなる。

　ここで、一次線間電圧V₁を基準とすると、二次電流I₂による一次線電流I₁₂＝70Aは誘導性負荷によるものであるため、V₁より進み電流である。題意より誘導性負荷は力率0.8であるので、一次線電流I₁₂のV₁と同相成分はI₁₂×0.8＝56Aとなる。また、三平方の定理より、一次線電流I₁₂がV₁より90°進む成分はI₁₂×0.6＝42Aとなる。

　いま、二次電流I₃による一次線電流をI₁₃＝42Aはコンデンサによるものであるため、V₁より90°遅れの電流である。これらをベクトル図で表すと、下図のようになる。

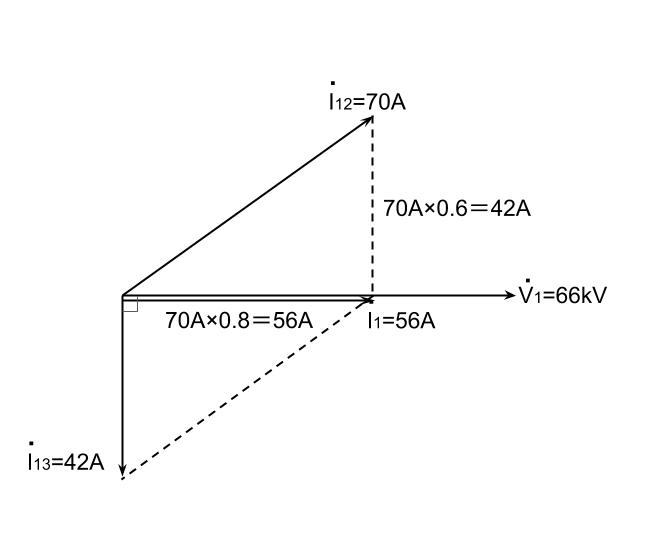
図からわかるように、二次電流I₂による一次線電流I₁₂＝70Aと、二次電流I₃による一次線電流I₁₃＝42Aの合成電流I₁＝56Aとなる。