電験３種過去問【2021年理論 問14】

解答

（５）

解説

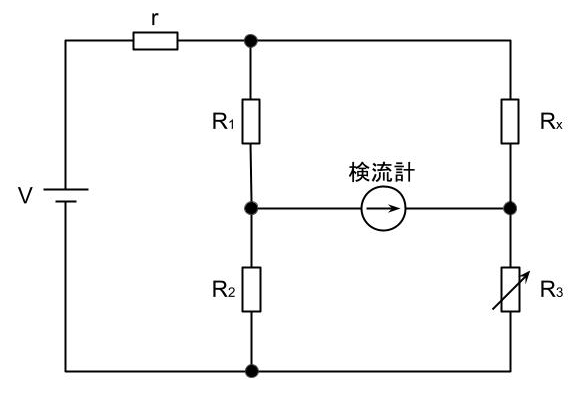
ブリッジ回路の検流計に電流が流れない、平衡条件を満足するには

$\displaystyle R_2 R_x=R_1 R_3$

となる。つまり、平衡条件を満足するときの未知の抵抗R_x[Ω]は、

$\displaystyle R_x=\frac{R_1 R_3}{R_2}$

題意より、既知抵抗R₁、R₂、R₃の各誤差は$\displaystyle ΔR_1=ε_1 R_1$、$\displaystyle ΔR_2=ε_2 R_2$、$\displaystyle ΔR_3=ε_3 R_3$となる。

未知抵抗R_x[Ω]の誤差は、既知抵抗R₁、R₂、R₃の各誤差からの影響のみであるので、誤差を含めた未知抵抗の値R_xε[Ω]は

$\displaystyle R_{xε}=\frac{(R_1+ΔR_1)(R_3+ΔR_3)}{R_2+ΔR_2}$

$\displaystyle =\frac{(R_1+ε_1 R_1)(R_3+ε_3 R_3)}{R_2+ε_2 R_2}$

$\displaystyle =\frac{(R_1(1+ε_1))(R_3(1+ε_3))}{R_2(1+ε_2)}$

$\displaystyle =\frac{R_1 R_3}{R_2}\frac{(1+ε_1)(1+ε_3)}{1+ε_2}$

$\displaystyle =R_x\frac{(1+ε_1)(1+ε_3)}{1+ε_2}$

したがって、未知抵抗の誤差率$\displaystyle ε_x$は

$\displaystyle ε_x=\frac{R_{xε} -R_x}{R_x}$

$\displaystyle =\frac{R_x\frac{(1+ε_1)(1+ε_3)}{1+ε_2} -R_x}{R_x}$

$\displaystyle =\frac{R_x(\frac{(1+ε_1)(1+ε_3)}{1+ε_2} -1)}{R_x}$

$\displaystyle =\frac{(1+ε_1)(1+ε_3)}{1+ε_2} -1$

$\displaystyle =\frac{(1+0.01)(1+0.02)}{1-0.01}-1$

$\displaystyle =0.041$