Loading [MathJax]/extensions/tex2jax.js
// google adsence用 電験３種過去問【2021年理論 問13】 | 電気主任技術者のいろは

電験３種過去問【2021年理論 問13】

2022年4月24日

【電子回路】FETの簡易等価回路《計算問題》

　図は、電界効果トランジスタ（FET）を用いたソース接地増幅回路の簡易小信号交流等価回路である。この回路の電圧増幅度\(\displaystyle A_v=\left|\frac{v_o}{v_i}\right|\)を近似する式として、正しいものを次の(1)～(5)のうちから一つ選べ。ただし、図中のS,G,Dはそれぞれソース,ゲート,ドレインであり、vi[V],vo[V],vgs[V]は各部の電圧、gm[S]はFETの相互コンダクタンスである。また、抵抗rd[Ω]は抵抗RL[Ω]に比べて十分大きいものとする。

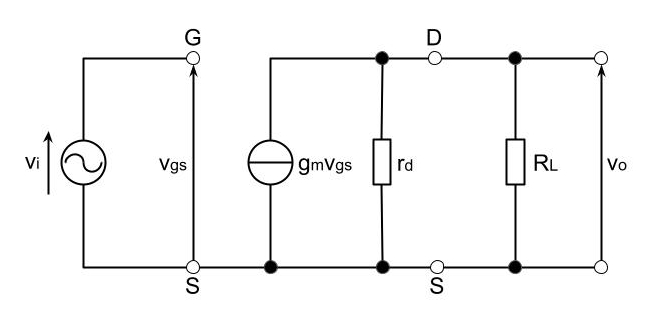
（１）\(\displaystyle g_m R_L\)（２）\(\displaystyle g_m r_d\)（３）\(\displaystyle g_m(R_L +r_d)\)（４）\(\displaystyle \frac{g_m r_d}{R_L}\)（５）\(\displaystyle \frac{g_m R_L}{R_L +r_d}\)

解答と解説はこちら

解答

（１）

解説

\(\displaystyle v_i\)[V]は、ゲート-ソース間電圧\(\displaystyle v_{gs}\)[V]であるので、

\(\displaystyle v_i=v_{gs}\text{[V]}\)

ドレイン側へは、電流源より\(\displaystyle g_m v_{gs}\)[A]の電流が流れるので、抵抗\(\displaystyle R_L\)[Ω]へ分流する電流\(\displaystyle i_{R_L}\)[A]は

\(\displaystyle i_{R_L}=g_m v_{gs}\left( \frac{r_d}{R_L +r_d}\right)\text{[A]}\)

\(\displaystyle v_o\)[V]は、抵抗\(\displaystyle R_L\)[Ω]にかかる電圧であるので、

\(\displaystyle v_o=i_{R_L} R_L\)

\(\displaystyle =g_m v_{gs}\left( \frac{r_d}{R_L +r_d}\right)R_L\text{[V]}\)

題意より、\(\displaystyle r_d>>R_L\)なので、\(\displaystyle (R_L +r_d)≒r_d\)と考えると

\(\displaystyle v_o=g_m v_{gs}\left( \frac{r_d}{r_d}\right)R_L\)

\(\displaystyle =g_m v_{gs}R_L\text{[V]}\)

したがって、電圧増幅度\(\displaystyle A_v\)は

\(\displaystyle A_v=\left|\frac{v_o}{v_i}\right|\)

\(\displaystyle =\left|\frac{g_m v_{gs}R_L}{v_{gs}}\right|\)

\(\displaystyle =g_m R_L\)

<<前問　　次問>>

 

電験３種過去問理論過去問, 電験3種, 理論, 電子回路, 2021年

Posted by ちゅん