電験３種過去問【2022年(上期)機械 問16】

解答

（a）:（4）が正しい。
（b）:（3）が正しい。

解説

(a)　電流が流れるデバイスの組合せは、
➀t = 0 ～ T/4の区間では、Q₁-Q₂ のIGBT素子が導通するが、これより前の区間（下の➃に相当する）でインダクタンスに蓄えられたエネルギーにより、前の区間で流れていた（下の➃に相当する）電流 -i_a が流れ続ける。従って、D₁-D₂ のダイオードに電流が流れる。
➁t = T/4 ～ T/2の区間では、Q₁-Q₂ のIGBT素子が導通しており、これらの素子に電流 i_a が流れる。
➂t = T/2 ～ 3T/4の区間では、Q₃-Q₄ のIGBT素子が導通するが、前の➁区間中でインダクタンスに蓄えられたエネルギーにより、➁の区間で流れていた電流 i_a が流れ続ける。従って、D₃-D₄ のダイオードに電流が流れる。
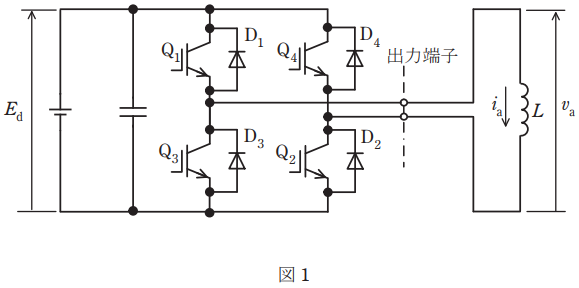
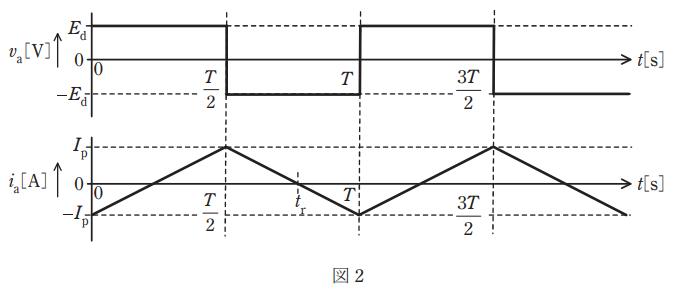
➃t = 3T/4 ～ Tの区間では、Q₃-Q₄ のIGBT素子が導通しており、これらの素子に電流 -i_a が流れる。

時刻 t = T/2 [s] の直前では Q₁ 及び Q₂ がオンしており、出力電流は直流電源から Q₁ →負荷→ Q₂ の経路で流れている。t = T/2 [s]で IGBT Q₁ 及び Q₂ のゲート信号をオフにするとともに Q₃ 及び Q₄ のゲート信号をオンにした。その直後（図２で、t = T/2 [s] から、出力電流が 0 A になる t = t_r [s] までの期間）、出力電流が流れるデバイスは上記➂となる。

(b)　コイルに電流を流した時発生する電圧を考える。

図１の回路において E_d = 100V 、L = 10 mH 、T = 0.02 s とする。t = 0 s における電流値を -I_p として、t = T/2 [s] における電流値を I_p としたとき、 I_p の値 [A] を求める。

インダクタンス L [H]のコイルに、電流 i [A]が流れるとき、コイルに発生する電圧v [V]は、
\(\displaystyle v=L\frac{di}{dt}\)[V]

上のコイルに流れる電流と電圧の関係より、図２において v = E_d = 100V 、L = 10 mH 、Δt = T/2 = 0.01 s 、Δi = { I_p– ( -I_p )} = 2I_p として、 I_p の値 [A] を求めると、
\(\displaystyle v=L\frac{\Delta i}{\Delta t}\)
∴\(\displaystyle 100=10\times 10^{-3}\frac{2I_p}{0.01}\)
∴\(\displaystyle I_p=50\)[A]