電験3種過去問【2022年(下期)機械 問15】
【自動制御】RLC回路の伝達関数とボード線図《計算問題》
図は、抵抗、インダクタンス、キャパシタンスで構成されたRLC回路である。次の(a)及び(b)の問に答えよ。
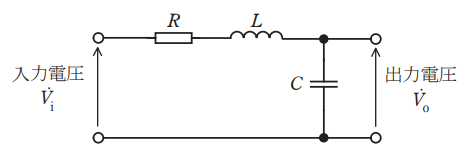
(a) 図において、入力電圧\(\dot{V}_i\)に対する、出力電圧\(\dot{V}_o\)の伝達関数\(\displaystyle G(j\omega)(=\frac{\dot{V}_o}{\dot{V}_i})\)を求め、正しいものを次の(1)~(5)のうちから一つ選べ。
\(\displaystyle (1) \frac{1}{1+\omega^2LC+j\omega CR}\) \(\displaystyle (2) \frac{1}{1-\omega^2LC+j\omega CR}\) \(\displaystyle (3) \frac{\sqrt{LC}}{1+\omega^2LC+j\omega CR}\) \(\displaystyle (4) \frac{\sqrt{LC}}{1-\omega^2LC+j\omega CR}\) \(\displaystyle (5) \frac{\omega^2LC}{\omega^2LC-1-j\omega CR}\)
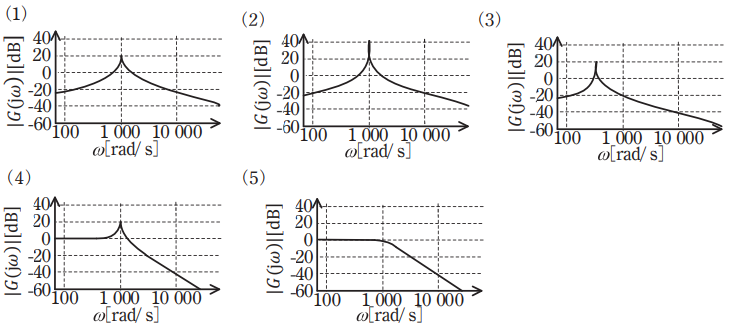
(b) 図において、R=1Ω、L=0.01H、C=100μF とした場合、(a)で求めた伝達関数を表すボード線図(ゲイン特性図)として、最も近いものを次の(1)~(5)のうちから一つ選べ。

ディスカッション
コメント一覧
まだ、コメントがありません