電験３種過去問【2019年法規 問12】

解答 

（a）：（５）
（b）：（３）

解説

（a）進相コンデンサ設備を高圧電路に接続したとき、１相分は下図のような回路になる。
※１相分の電圧は\(\displaystyle \frac{6600}{\sqrt3}\)[V]であるが、1相分の計算後に線間電圧に戻す（\(\displaystyle \times\sqrt3\)倍する）ため、簡単のため6600Vとした

SCの端子電圧V_C[V]を求める。題意より、X_L[Ω]はX_C[Ω]の6％であるので、

　X_L=0.06X_C　

進相コンデンサ設備の合成リアクタンス\(\displaystyle \dot{X}_{LC}\)[Ω]は、

\(\displaystyle \dot{X}_{LC}=\dot{X}_{L}+\dot{X}_{C}=jX_L-jX_C\)

\(\displaystyle =j0.06X_C-jX_C=-j0.94X_C\)[Ω]

進相コンデンサを流れる電流\(\displaystyle \dot{I}_{LC}\)[A]は、

\(\displaystyle \dot{I}_{LC}=\frac{\dot{V}}{\dot{X}_{LC}}\)

\(\displaystyle =\frac{6600}{-j0.94X_C}=j\frac{6600}{0.94X_C}\)[A]

求めるSCの端子電圧\(\displaystyle \dot{V}_{C}\)[V]は、

\(\displaystyle \dot{V}_{C}=\dot{X}_{C}\times\dot{I}_{LC}\)

\(\displaystyle =-jX_{C}\times j\frac{6600}{0.94X_C}\)

\(\displaystyle =\frac{6600}{0.94}=7021\)[V]

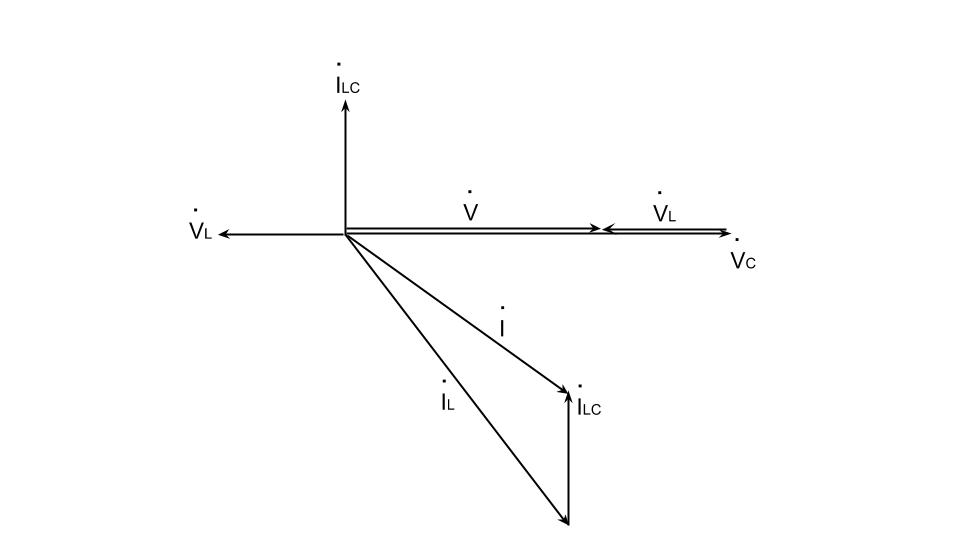
それぞれの、電流と電圧の関係は下図のようになる。

 

（b）有効電力300kWで遅れ力率0.6のとき、皮相電力は300/0.6＝500[kVA]となる。このときの無効電力は\(\displaystyle \sqrt{500^2-300^2}=400\)[kVar]となる。

有効電力300kWで遅れ力率0.8に改善したとき、皮相電力は300/0.8＝375[kVA]となる。このときの無効電力は\(\displaystyle \sqrt{375^2-300^2}\)＝225[kVar]となる。

これらの関係は下図のようになる。

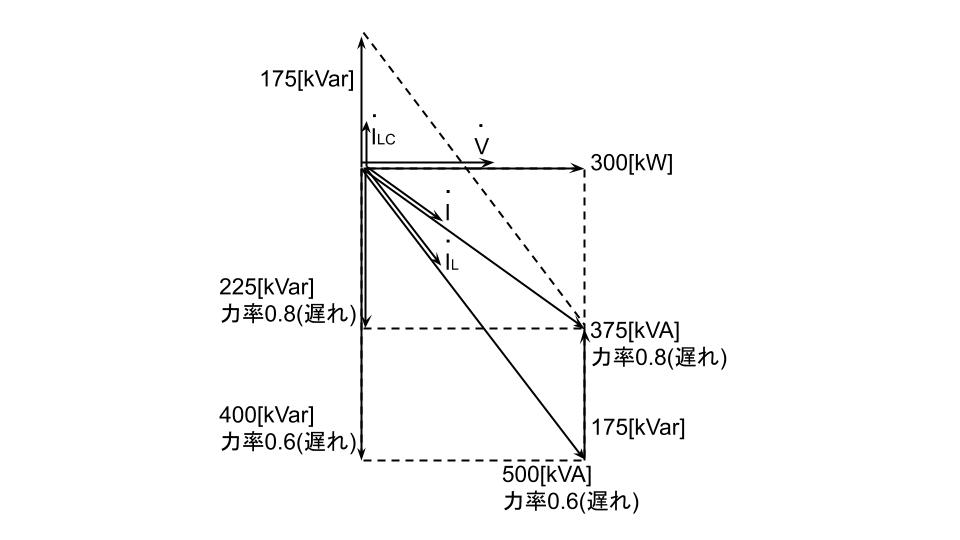
上図のように、力率0.6から0.8へ改善するには、400-225＝175[kVar]の無効電力が進相コンデンサから供給されている。

前問(a)のベクトル図からわかるように、V_LとV_Cは逆向き(V_L＜V_C)である。\(\displaystyle V_C-V_L\)によって供給される無効電力が175[kVar]となるので、コンデンサSCの容量Q_SC[kVar]との比は、その電圧の比と等しい。

\(\displaystyle \frac{175}{Q_{SC}}=\frac{V_C-V_L}{V_C}\)

\(\displaystyle =\frac{6600}{7021}\)

\(\displaystyle Q_{SC}=175\times\frac{7021}{6600}=186\)

　Q_SC＝186[kVar]