電験２種過去問【2021年理論 問6】

解答

(１)：（リ）
(２)：（ヘ）
(３)：（ハ）
(４)：（ル）
(５)：（ロ）

解説

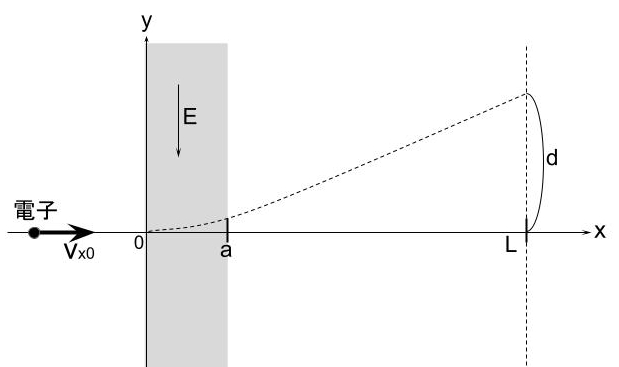
　図にように、真空中を電子（質量ｍ、電荷量‐e、e>0）がｘ軸上をx<0の領域から一定速度\(\displaystyle v_{x0}(>0)\)で運動している。領域\(\displaystyle 0≦x≦a\)には、図に示すようにy軸の負の方向に均一な電界\(\displaystyle E(>0)\)がかかっており、それ以外の領域では電界がないものとする。

電子のｘ座標がx=0からx=aに達するまでにかかる時間は\(\displaystyle \frac{距離}{速さ}=\frac{a}{v_{x0}}\)である。

領域\(\displaystyle 0≦x≦a\)では、電子は電界から力F=\(\fbox{eE}\)を受けてy方向に偏向する。運動の第2法則からy方向の運動方程式は

\(\displaystyle F=ma=m\frac{dv_y}{dt}= \)\(\fbox{eE}\)

と表される。ただし、\(\displaystyle v_y\)は速度のy方向成分、aは加速度のy方向成分を表す。

微分方程式を解くことにより、電子のx座標がx=aに到達したときの\(\displaystyle v_y\)を求める。

\(\displaystyle m\frac{dv_y}{dt}=eE \)

\(\displaystyle \frac{dv_y}{dt}=\frac{eE}{m} \)

両辺を積分して、一般解を求めると

\(\displaystyle v_y=\int\frac{dv_y}{dt}dt=\int\frac{eE}{m}dt=\frac{eE}{m}t+v_{y0} \) …①

t＝0における、初速度\(\displaystyle v_{y0}＝0 \)であるので、

\(\displaystyle v_y=\frac{eE}{m}t \)

x=0(t=0)からx=aに達するまでの時間\(\displaystyle t=\frac{a}{v_{x0}}\)を代入すると

\(\displaystyle v_y=\frac{eE}{m}\frac{a}{v_{x0}} \)

つまり、\(\displaystyle v_y=\frac{eE}{m}\frac{a}{v_{x0}}\)となる。

次に、電子のx座標がx=aに到達したときの電子のy座標を求める。

①式より、

\(\displaystyle v_y=\frac{eE}{m}t+v_{y0} \)

y座標と速度\(\displaystyle v_y \)の関係は、

\(\displaystyle v_y=\frac{dy}{dt}=\frac{eE}{m}t+v_{y0} \)

両辺を積分して、一般解を求めると

\(\displaystyle y=\int\frac{dy}{dt}dt=\int\left(\frac{eE}{m}t+v_{y0}\right)dt \)

\(\displaystyle =\frac{1}{2}\frac{eE}{m}t^2+v_{y0}t+y_0 \)

t＝0における、初速度及び初期座標は\(\displaystyle v_{y0}＝0, y_0=0 \)であるので、

\(\displaystyle y=\frac{1}{2}\frac{eE}{m}t^2 \)

x=0(t=0)からx=aに達するまでの時間\(\displaystyle t=\frac{a}{v_{x0}}\)を代入すると

\(\displaystyle y=\frac{1}{2}\frac{eE}{m}\left(\frac{a}{v_{x0}}\right)^2 \)

つまり、\(\displaystyle y=\frac{eE}{2m}\left(\frac{a}{v_{x0}}\right)^2\)となる。

領域x>aでは、電子の運動はx,y方向共に等速運動となることから、電子が\(\displaystyle x=L(>a)\)に到達した際のy座標をdとすると、

\(\displaystyle d=y+v_y\frac{(L-a)}{v_{x0}} \)

\(\displaystyle =\frac{eE}{2m}\left(\frac{a}{v_{x0}}\right)^2+\frac{eE}{m}\frac{a}{v_{x0}}\frac{(L-a)}{v_{x0}} \)

\(\displaystyle =\frac{eE}{2m}\frac{(2aL-a^2)}{v_{x0}^2} \)

\(\displaystyle =\frac{eE}{2m}\frac{a(2L-a)}{v_{x0}^2} \)

よって、\(\displaystyle d=\frac{eE}{2m}\frac{a(2L-a)}{v_{x0}^2} \)となる。