電験２種過去問【2020年理論 問8】

解答

解説

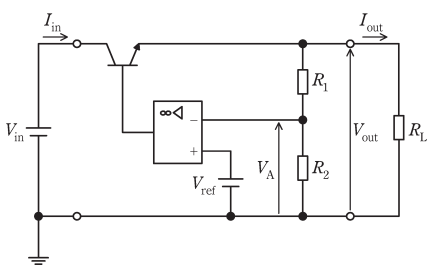
　図の回路の入力電圧と出力電圧をそれぞれ$V_{in}$と$V_{out}$とする。$R_L$は負荷であり、$R_L$を流れる電流を出力電流$I_{out}$とする。演算増幅器は理想的な特性を有し、演算増幅器の入力端子には電流が流れないとする。このとき$V_A$は$V_{out}$、$R_1$及び$R_2$を用いて、
　$\displaystyle V_A=(ﾖ)\frac{R_2}{R_1+R_2}V_{out}$　…①
と書ける。また、負帰還のかかった演算増幅器の入力端子間の電位差は零となるため、
　$V_A=(ﾎ)V_{ref}$　…②
と表される。①及び②式から$V_A$を消去すると出力電圧は、
　$V_{out}=(ﾆ)\displaystyle\frac{R_1+R_2}{R_2}V_{ref}$　…③
と求められる。③式よりこの回路の出力電圧は基準電圧$V_{ref}$と抵抗$R_{1}$と$R_{2}$のみで定まり、出力電流$I_{out}$や入力電圧$V_{in}$の大きさによらず一定となることがわかる。
　通常$R_{1}$と$R_{2}$は$R_{L}$に比べ十分に大きい値なので、入力電流$I_{in}$は$I_{out}$と等しいと近似できる。このとき回路の入力電力と出力電力の差は

$\displaystyle V_{in}I_{in}-V_{out}I_{out}≒V_{in}I_{out}-V_{out}I_{out}=$

$(ﾍ)(V_{in}-V_{out})I_{out}$となり、主に$\fbox{(ﾊ)トランジスタ}$で消費される。