電験２種過去問【2020年理論 問5】

解答

解説

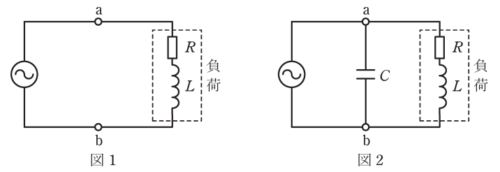
　図１の回路において、負荷の抵抗はR＝3Ω、有効電力Pは600W、力率は0.6である。また、電源の角周波数はωである。

この負荷の無効電力Qを求める。

力率\(\displaystyle \cos\theta =0.6=\frac{600}{S}\)であるので、

\(\displaystyle S=1000\) [VA]

\(\displaystyle S^2=P^2+Q^2\)であるので、

\(\displaystyle Q^2=S^2-P^2=1000^2-600^2=640000\)

\(\displaystyle Q=800\) [Var]

この負荷の無効電力は\(\fbox{(ﾙ)800}\)var

負荷のリアクタンスを求めると、

\(\displaystyle R:\omega L=P:Q\)であるので

\(\displaystyle \omega L=\frac{RQ}{P}\)

\(\displaystyle =\frac{3\times800}{600}=4\)

ωL＝\(\fbox{(ﾇ)4}\)Ωである。

　図２のように、図１の回路の端子a-bにキャパシタCを接続すると、電源からみた回路の合成負荷のアドミタンスは\(\displaystyle \dot{Y}=\frac{R}{R^2+(\omega L)^2}+j\left(\omega C-\frac{\omega L}{R^2+(\omega L)^2}\right)\)となる。

図２において電源から見た回路の合成負荷の力率を１とした。このとき、キャパシタCのサセプタンスは、\(\displaystyle \omega C-\frac{\omega L}{R^2+(\omega L)^2}=0\)であるから

\(\displaystyle \omega C=\frac{\omega L}{R^2+(\omega L)^2}\)

\(\displaystyle =\frac{4}{3^2+4^2}\)

ωC＝\(\fbox{(ｲ)0.16}\)Sである。

　キャパシタCを接続して合成負荷の力率を１にした後に、電源の角周波数ωを\(\displaystyle \frac{1}{2}\)倍にすると、電源からみた回路の合成負荷\(\displaystyle \dot{Y}\)は、

\(\displaystyle \dot{Y}=\frac{R}{R^2+(\frac{1}{2}\omega L)^2}+j\left(\frac{1}{2}\omega C-\frac{\frac{1}{2}\omega L}{R^2+(\frac{1}{2}\omega L)^2}\right)\)

\(\displaystyle =\frac{3}{3^2+(\frac{1}{2}\times4)^2}+j\left(\frac{1}{2}\times0.16-\frac{\frac{1}{2}\times4}{3^2+(\frac{1}{2}\times4)^2}\right)\)

\(\displaystyle =0.231-j0.071\)

つまり\(\displaystyle \tan\theta =\frac{-0.071}{0.231}\)であり、

\(\displaystyle \tan^2\theta+1 =\frac{1}{\cos^2\theta}\)より

\(\displaystyle \cos\theta =0.952\)

回路側からみた合成負荷は、\(\displaystyle \dot{Y}=0.231-j0.071\)であるので、

\(\displaystyle \dot{Z}=\frac{1}{0.231-j0.071}\)

\(\displaystyle =\frac{0.231+j0.071}{(0.231+j0.071)(0.231-j0.071)}\)

\(\displaystyle =\frac{0.231+j0.071}{0.058}\)

つまり、力率\(\fbox{(ﾜ)0.952}\)の\(\fbox{(ﾁ)誘導性}\)負荷となる。