電験2種過去問【2020年電力管理 問3】
【送電】対称座標法を用いた1線地絡故障計算《論説問題》
対称座標法を用いた1線地絡故障の計算に関して、次の問に答えよ。
図のような送受電端の変圧器の中性点をそれぞれ Re の抵抗で接地したこう長 20 km、電圧 66 kV、周波数 50 Hz の三相3線式1回線送電線路がある。
その a 相1線が Rf の抵抗を通じて地絡を生じた場合の地絡電流を求めたい。
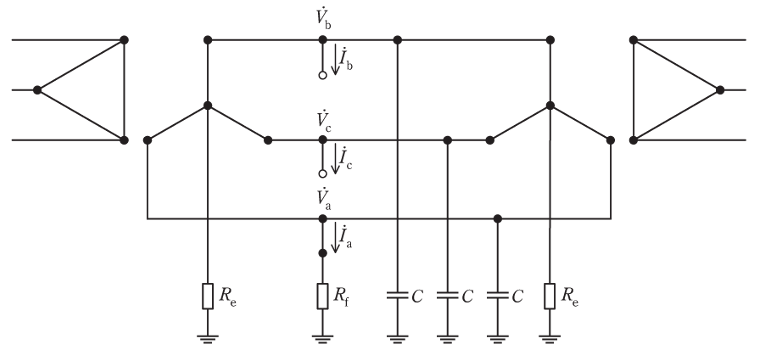
- 地絡電流\(\dot{I}_g\)を、a 相の無負荷電圧\(\dot{E}_a\)、この送電回路の故障点から見た零相インピーダンス\(\dot{Z}_0\)、正相インピーダンス\(\dot{Z}_1\)、逆相インピーダンス\(\dot{Z}_2\)、及び、地絡点の抵抗 Rf で表せ。
なお、故障点での各相電圧、各相電流を図に示すように\(\dot{V}_a,\dot{V}_b,\dot{V}_c,\dot{I}_a,\dot{I}_b,\dot{I}_c\)とし、それを対称成分に変換したものを\(\dot{V}_0,\dot{V}_1,\dot{V}_2,\dot{I}_0,\dot{I}_1,\dot{I}_2\)としたとき、以下の関係となる。
\(\begin{eqnarray}
\dot{V}_0&=&-\dot{Z}_0\dot{I}_0,\\
\dot{V}_1&=&\dot{E}_a-\dot{Z}_1\dot{I}_1,\\
\dot{V}_2&=&-\dot{Z}_2\dot{I}_2
\end{eqnarray}\)
また、故障条件から以下の関係となる。
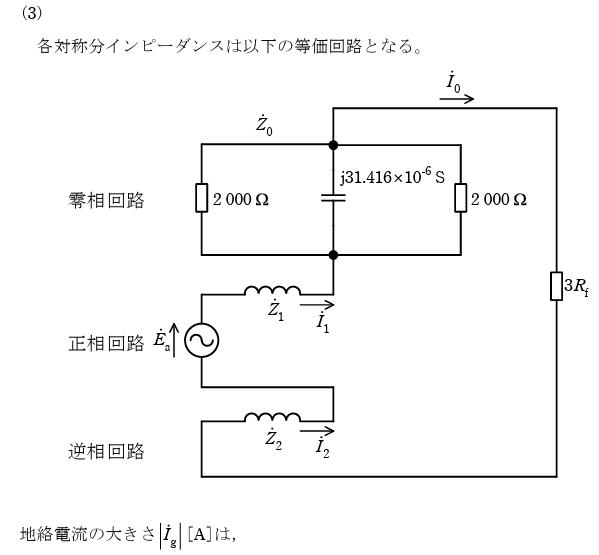
\(\dot{I}_b=\dot{I}_c=0,\dot{V}_a=\dot{I}_a\dot{R}_f\) - 零相インピーダンス\(\dot{Z}_0\)、正相インピーダンス\(\dot{Z}_1\)、逆相インピーダンス\(\dot{Z}_2\)をそれぞれ求めよ。ただし、1線当たりの対地静電容量 C は 0.005 μF/km、変圧器の中性点の抵抗 Re は\(\dfrac{2000}{3}\)Ωとして、その他のインピーダンス、また負荷電流は無視するものとする。
なお、π = 3.1416 とする。 - 小問 2. の条件に加えて、地絡点の抵抗 Rf が 10 Ωの場合における地絡電流の大きさ|\(\dot{I}_g\)| [A] を求めよ。
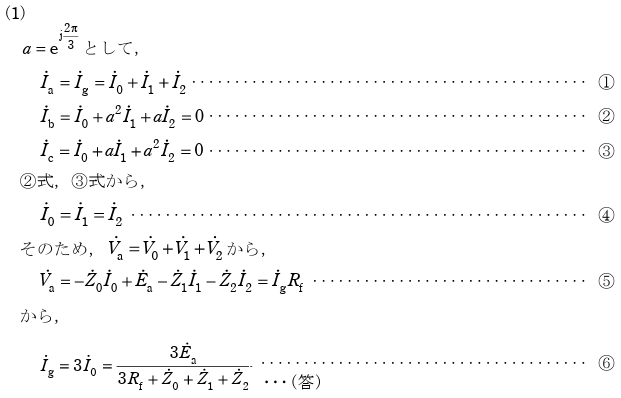



ディスカッション
コメント一覧
まだ、コメントがありません