電験１種過去問【2018年機械制御問4】

2018年12月1日2024年6月9日

【自動制御】現代制御におけるフィードバック制御系の解析《計算問題》

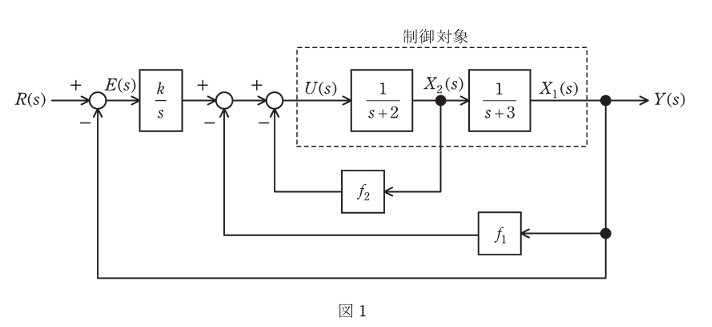
　図１のフィードバック制御系について、次の問に答えよ。ただし、以下の設問において用いる　x₁(t), x₂(t), u(t), y(t), r(t), e(t) 及び z(t) のラプラス変換をそれぞれ X₁(s), X₂(s), U(s), Y(s), R(s), E(s) 及び Z(s) で表す。
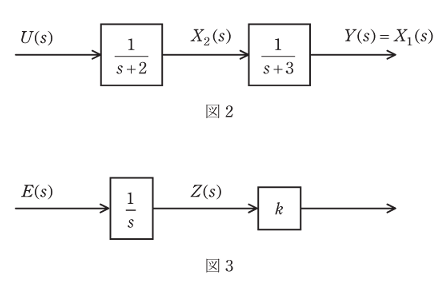
（１）図１の制御対象部分を示す図２において、状態変数を x₁(t)、 x₂(t)、制御対象の入力と出力をそれぞれ u(t)、y(t) とする。このとき、状態ベクトル x(t)=[x₁(t)　x₂(t)]^Tが満たす次の状態空間表現
　\(\boldsymbol{\dot{x}}(t)\)=Ax(t)+bu(t), y(t)=cx(t)
における A, b, c を求めよ。
（２）図１の積分器を図３のように書き直して、変数 Z(s) を新たに設けるとき、この時間関数 z(t) は、関係式
　\(\dot{z}(t)\)=r(t)-y(t)=r(t)-cx(t)
を満たす。また、入力 u(t) は次のように書くことができる。
　u(t)=-fx(t)+kz(t), f=[f₁　f₂]
積分器の出力である z(t) を状態変数として取り込み、状態ベクトルを \(\boldsymbol{\overline{x}}(t)\)=[x₁(t)　x₂(t)　z(t)]^T に拡大すると、図１のフィードバック制御系は次の状態空間表現
　 \(\boldsymbol{\dot{\overline{x}}}(t)=\boldsymbol{\overline{A}\overline{x}}(t)+\boldsymbol{\overline{b}}r(t)\), \(y(t)=\boldsymbol{\overline{c}\overline{x}}(t)\)
　で記述できる。 \(\boldsymbol{\overline{A}},\boldsymbol{\overline{b}},\boldsymbol{\overline{c}}\)を A, b, c, k, f, 0 及び 1 を用いて表せ。
（３）k=1, f₁=1, f₂=1 として、上記小問(2)の行列\(\overline{A}\)の固有値を与える特性多項式を示せ。
（４）k=1, f₁=1, f₂=1 として、図１のブロック線図の目標値 R(s) から出力 Y(s) までの伝達関数を求めよ。