Processing math: 4%
// google adsence用 電験２種過去問【2019年理論 問6】 | 電気主任技術者のいろは

電験２種過去問【2019年理論 問6】

2022年7月10日

【電気回路】直流回路に流れる電流の計算《空所問題》

　次の文章は、直流電源と抵抗からなる回路の電流に関する記述である。文中の\fbox{空所欄}に当てはまる最も適切なものを解答群の中から選べ。
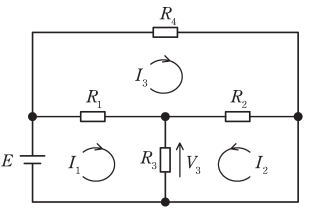
　図の抵抗回路の閉路電流I_1,I_2,I_3は、閉路方程式を解いて求めることができるが、以下の手順で求めることもできる。

  1. 　I_3は、R_4の両端の電位差に注意すると、 I_3=\fbox{（１）}。
  2. 　R_3での電圧降下V_3の式は、
    　　\displaystyle V_3=\frac{1}{R_1+\frac{R_2R_3}{R_2+R_3}}\times\fbox{（２）}\times E
    となる。
  3. 　I_1,I_2,I_3を使うと、
    　　E-V_3=R_1(　\fbox{（３）}　)
    　　V_3=R_2(　\fbox{（４）}　)
    である。

以上を利用すれば、
　　\displaystyle I_1=E\left(\frac{1}{R_4}+\frac{R_2+R_3}{R_1R_2+R_2R_3+R_3R_1}\right)
　　I_2=\fbox{（５）}
が得られる。

［問６の解答群］

\small{\begin{array}{ccc} (ｲ)&\displaystyle E\left(-\frac{1}{R_4}-\frac{R_3}{R_1R_2+R_2R_3+R_3R_1}\right)&(ﾛ)&I_1-I_3&(ﾊ)&-I_2-I_3\\ (ﾆ)&\displaystyle\frac{R_1R_2}{R_1+R_2}&(ﾎ)&I_3+I_1&(ﾍ)&\displaystyle\frac{R_2R_3}{R_2+R_3}\\ (ﾄ)&\displaystyle E\left(-\frac{R_3}{R_1R_2+R_2R_3+R_3R_1}\right)&(ﾁ)&\displaystyle\frac{R_2R_4}{R_2+R_4}&(ﾘ)&\displaystyle\frac{E}{R_1+R_2+R_4}\\ (ﾇ)&I_2&(ﾙ)&\displaystyle\frac{E}{R_1+R_2}&(ｦ)&I_3-I_1\\ (ﾜ)&\displaystyle E\left(\frac{1}{R_4}-\frac{R_3}{R_1R_2+R_2R_3+R_3R_1}\right)&(ｶ)&\displaystyle\frac{E}{R_4}&(ﾖ)&I_1\\ \end{array}}

解答と解説はこちら

解答

\small{\begin{array}{cc} \hline(1)&(ｶ)&\displaystyle\frac{E}{R_4}\\ \hline(2)&(ﾍ)&\displaystyle\frac{R_2R_3}{R_2+R_3}\\ \hline(3)&(ﾛ)&I_1-I_3\\ \hline(4)&(ﾊ)&-I_2-I_3\\ \hline(5)&(ｲ)&\displaystyle E\left(-\frac{1}{R_4}-\frac{R_3}{R_1R_2+R_2R_3+R_3R_1}\right)\\ \hline\end{array}}

解説

　図の抵抗回路の閉路電流I_1,I_2,I_3は、閉路方程式を解いて求めることができるが、以下の手順で求めることもできる。

  1. 　I_3は、R_4の両端の電位差に注意すると、 I_3=(ｶ)\displaystyle\frac{E}{R_4}。
  2. 　R_3での電圧降下V_3の式は、
    　　\displaystyle V_3=\frac{1}{R_1+\frac{R_2R_3}{R_2+R_3}}\times(ﾍ)\frac{R_2R_3}{R_2+R_3}\times E
    となる。
  3. 　I_1,I_2,I_3を使うと、
    　　E-V_3=R_1(　(ﾛ)I_1-I_3　)
    　　V_3=R_2(　(ﾊ)-I_2-I_3　)
    である。

以上を利用すれば、
　　\displaystyle I_1=E\left(\frac{1}{R_4}+\frac{R_2+R_3}{R_1R_2+R_2R_3+R_3R_1}\right)
　　I_2=(ｲ)\displaystyle E\left(-\frac{1}{R_4}-\frac{R_3}{R_1R_2+R_2R_3+R_3R_1}\right)
が得られる。

<<前問　　次問>>

 

電験２種過去問理論過去問, 電験2種, 理論, 電気回路, 2019年

Posted by ちゅん