電験２種過去問【2020年理論 問6】

解答

解説

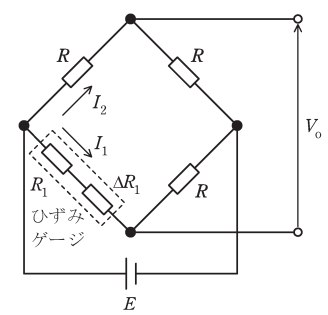
　図は、ひずみにより微小な抵抗変化を生じるひずみゲージを用いた測定回路である。このような抵抗の測定には、図のような$\fbox{(ﾛ)ホイートストン}$ブリッジの原理が使用される。
　図において、直流電圧源をE、回路の電流$I_1,I_2$とする。ひずみがなく、ひずみゲージの固定抵抗$R_1$の変化$\Delta R_1$が$\Delta R_1=0$の場合、ブリッジの出力電圧$V_0$を$R_1,R,E$を用いて表すと、

$\displaystyle V_0=\frac{R}{2R}E-\frac{R}{R_1+R}E$

$\displaystyle =\left(\frac{1}{2}-\frac{R}{R_1+R}\right)E$

$\displaystyle =\frac{(R_1+R)-2R}{2(R_1+R)}E$

$\displaystyle =\frac{R_1-R}{2(R_1+R)}E$

　$\displaystyle V_0=(ﾊ)\frac{R_1-R}{2(R_1+R)}E$　…①
となる。ただし、周囲温度の変化による各抵抗の変化は無視できるものとする。
　次に、ひずみが生じ、$R_1$が$R_1+\Delta R_1$になった場合を考える。
$R_1=R$となるようなひずみゲージを選べば、①式より$V_0$は

$\displaystyle V_0=\frac{R_1+\Delta R_1-R}{2(R_1+\Delta R_1+R)}E$

$\displaystyle =\frac{R+\Delta R_1-R}{2(R+\Delta R_1+R)}E$

$\displaystyle V_0=(ﾄ)\frac{\Delta R_1}{(4R+2\Delta R_1)}E$　…②
となる。ここで、通常　$R_1≫\Delta R_1$であることから、②式より$V_0$は
$\displaystyle V_0≒(ﾍ)\frac{\Delta R_1}{4R}E$
となり、$\Delta R_1$に比例した電圧が得られる。
　したがって、$R_1=R=100$Ω、E＝2Vであるとき、ある大きさのひずみにより、0.2％の抵抗増加が$R_1$に生じたとすれば、

$\displaystyle V_0=\frac{\Delta R_1}{4R}E$

$\displaystyle =\frac{100\times0.002}{4\times100}2$

$\displaystyle =0.001$ [V]

$\fbox{(ﾙ)1.0}$mVの出力電圧$V_0$が得られる。