電験３種過去問【2021年理論 問1】
【電磁気】平行板コンデンサの電界と電束《空所問題》
次の文章は、平行板コンデンサに関する記述である。
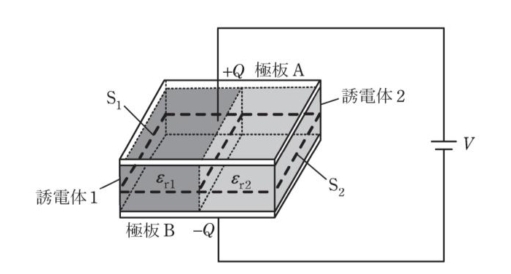
図のように、同じ寸法の直方体で誘電率の異なる二つの誘電体（比誘電率εr1の誘電体1と比誘電率εr2の誘電体2）が平行板コンデンサに充填されている。極板間は一定の電圧V[V]に保たれ、極板Aと極板Bにはそれぞれ+Q[C]と-Q[C]（Q＞０）の電荷が蓄えられている。誘電体１と誘電体２は平面で接しており、その境界面は極板に対して垂直である。ただし、端効果は無視できるものとする。
この平行板コンデンサにおいて、極板A,Bに平行な誘電体１、誘電体２の断面をそれぞれ面S1、面S2（面S1と面S2の断面積は等しい）とすると、面S1を貫く電気力線の総数（任意の点の電気力線の密度は、その点での電界の大きさを表す）は、面S2を貫く電気力線の総数の\(\fbox{（ア）}\)倍である。面S1を貫く電束の総数は、面S2を貫く電束の総数の\(\fbox{（イ）}\)倍であり、面S1と面S2を貫く電束の数の総和は\(\fbox{（ウ）}\)である。
上記の記述中の空白個所(ア)～(ウ)に当てはまる組合せとして、正しいものを次の（１）～（５）のうちから一つ選べ。
\(\small{\begin{array}{cccc}
&(ア)&(イ)&(ウ)\\
\hline(1)&1& \displaystyle \frac{ε_{r1}}{ε_{r2}}& Q\\
\hline(2)&1& \displaystyle \frac{ε_{r1}}{ε_{r2}}& \displaystyle \frac{Q}{ε_{r1}}+\frac{Q}{ε_{r2}}\\
\hline(3)&1& \displaystyle \frac{ε_{r2}}{ε_{r1}}& \displaystyle \frac{Q}{ε_{r1}}+\frac{Q}{ε_{r2}}\\
\hline(4)& \displaystyle \frac{ε_{r2}}{ε_{r1}} & 1& \displaystyle \frac{Q}{ε_{r1}}+\frac{Q}{ε_{r2}}\\
\hline(5)& \displaystyle \frac{ε_{r2}}{ε_{r1}} & 1& Q\\
\hline\end{array}}\)
https://archivelog.net/denken3-kakomon/
https://archivelog.net/denken/