電験3種過去問【2020年理論 問8】
【電気回路】RC交流回路の計算《計算問題》
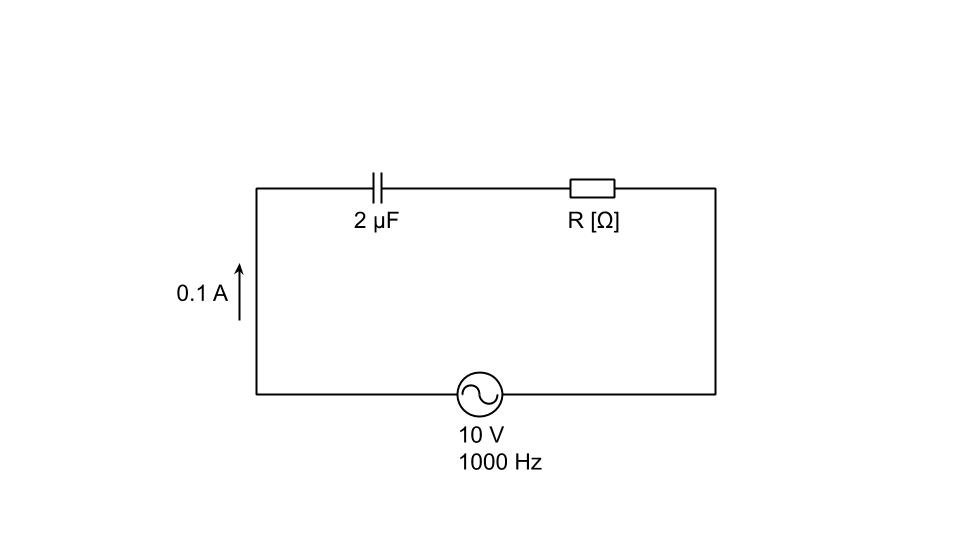
図のように、静電容量2μFのコンデンサ、R[Ω]の抵抗を直列に接続した。この回路に、正弦波交流電圧10V、周波数1000Hzを加えたところ、電流0.1Aが流れた。抵抗Rの値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
| (1)4.50 | (2)20.4 | (3)30.3 | (4)60.5 | (5)79.6 |
電験、電気その他のことをアーカイブするブログ
2022年11月26日
図のように、静電容量2μFのコンデンサ、R[Ω]の抵抗を直列に接続した。この回路に、正弦波交流電圧10V、周波数1000Hzを加えたところ、電流0.1Aが流れた。抵抗Rの値[Ω]として、最も近いものを次の(1)~(5)のうちから一つ選べ。

| (1)4.50 | (2)20.4 | (3)30.3 | (4)60.5 | (5)79.6 |
(4)
回路の合成インピーダンスは
\(\displaystyle |\dot{Z}|=\sqrt{R^2+(\frac{1}{2\pi fC})^2}\)
\(\displaystyle =\sqrt{R^2+(\frac{1}{2\pi \times 1000 \times 2\times 10^{-6}})^2}\)[Ω] …(1)
一方、電圧と電流から合成インピーダンスを求めると、
|Z|=10[V]/0.1[A]=100[Ω] …(2)
式(1)、式(2)より
\(\displaystyle \sqrt{R^2+(\frac{1}{2\pi \times 1000 \times 2\times 10^{-6}})^2}=100\)
\(\displaystyle R^2+(\frac{1}{2\pi \times 1000 \times 2\times 10^{-6}})^2=100^2\)
\(\displaystyle R^2=100^2-(\frac{1}{2\pi \times 1000 \times 2\times 10^{-6}})^2=3667\)
\(\displaystyle R=60.5\)[Ω]
したがって、回路中の抵抗R=60.5[Ω]となる。
【電動機応用】巻上機の電動機出力《計算問題》 巻上機によって質量1000kgの ...
【パワエレ】電力変換回路の出力電圧波形《正誤問題》 図に示す出力波形\(v_R ...
【照明】照度の定義と逆2乗の法則《空所問題》 次の文章は、照度の定義と逆2条の ...
【配電】配電線路の電圧降下と電流《計算問題》 図のような系統構成の三相3線式配 ...
【配電】高圧架空配電線路に関する知識《正誤問題》 高圧架空配電線路を構成する機 ...
ディスカッション
コメント一覧
まだ、コメントがありません