電験3種過去問【2020年理論 問6】
【電気回路】抵抗での消費電力計算《計算問題》
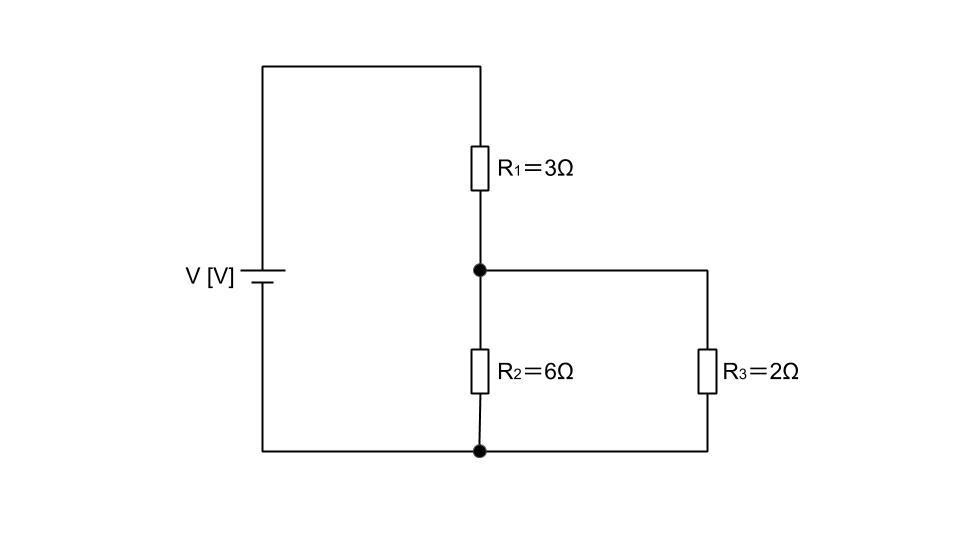
図のように、三つの抵抗R1=3Ω、R2=6Ω、R3=2Ωと電圧V[V]の直流電源からなる回路がある。抵抗R1、R2、R3の消費電力をそれぞれP1[W]、P2[W]、P3[W]とするとき、その大きさの大きい順として、正しいものを次の(1)~(5)のうちから一つ選べ。
| (1)P1>P2>P3 | (2)P1>P3>P2 | (3)P2>P1>P3 |
| (4)P2>P3>P1 | (5)P3>P1>P2 |
電験、電気その他のことをアーカイブするブログ
2022年4月24日
図のように、三つの抵抗R1=3Ω、R2=6Ω、R3=2Ωと電圧V[V]の直流電源からなる回路がある。抵抗R1、R2、R3の消費電力をそれぞれP1[W]、P2[W]、P3[W]とするとき、その大きさの大きい順として、正しいものを次の(1)~(5)のうちから一つ選べ。

| (1)P1>P2>P3 | (2)P1>P3>P2 | (3)P2>P1>P3 |
| (4)P2>P3>P1 | (5)P3>P1>P2 |
(2)
R2=6ΩとR3=2Ωの並列部分の合成抵抗R23[Ω]は
R23=R2R3/(R2+R3)=12/8=1.5[Ω]となる。
電源電圧V[V]はR1[Ω]とR23[Ω]の直列回路に接続されることになるので、R1[Ω]に掛かる電圧V1[V]と、R23[Ω]に掛かる電圧V23[V]は以下のようになる。
V1=R1/(R1+R23)×V=3V/4.5=0.67V[V]
V23=R23/(R1+R23)×V=1.5V/4.5=0.33V[V]
抵抗R[Ω]に電圧V[V]が与えられるときの消費電力P=V2/R[W]であるので、
P1=(0.67V)2/3=0.15V2[W]
P2=(0.33V)2/6=0.02V2[W]
P3=(0.33V)2/2=0.05V2[W]
従って、抵抗R1、R2、R3の消費電力は大きい順にP1>P3>P2となる。
【配電】単相3線式の特徴《記述問題》 一般的に低圧配電方式として広く使用されて ...
【送電】架空送電線路の構成要素に関する記述《正誤問題》 架空送電線路の構成要素 ...
【誘導機】三相誘導電動機の回転磁界に関する記述《正誤選択》 三相誘導電動機の回 ...
【電気回路】直流回路の抵抗に流れる電流計算《計算問題》 図のような直流回路にお ...
【パワエレ】三相インバータ、電圧波形作図、中性点電圧導出《計算問題》 図1は三 ...
ディスカッション
コメント一覧
まだ、コメントがありません