// google adsence用 電験３種過去問【2016年電力 問17】 | 電気主任技術者のいろは

電験３種過去問【2016年電力 問17】

2025年6月5日

【配電】バランサ接続前後の線路損失計算《計算問題》

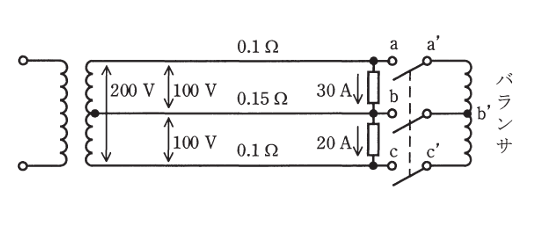
　図のような，線路抵抗をもった 100/200V 単相 3 線式配電線路に，力率が 100 % で電流がそれぞれ 30 A 及び 20 A の二つの負荷が接続されている。この配電線路にバランサを接続した場合について，次の(a)及び(b)の問に答えよ。
　ただし，バランサの接続前後で負荷電流は変化しないものとし，線路抵抗以外のインピーダンスは無視するものとする。

(a) バランサ接続後 a’-b’ 間に流れる電流の値 [A] として，最も近いものを次の(1)～(5)のうちから一つ選べ。

（1）5
（2）10
（3）20
（4）25
（5）30

(b) バランサ接続前後の線路損失の変化量の値 [W] として，最も近いものを次の(1)～(5)のうちから一つ選べ。

（1）20
（2）65
（3）80
（4）125
（5）145


「出典：平成28年度第三種電気主任技術者試験（電力）」

解答と解説はこちら

解答

(a):（1）が最も近い。
(b):（1）が最も近い。

解説

　バランサについての計算問題です。バランサの性質を理解していれば難しい問題ではありません。

(a) バランサ接続後 a’-b’ 間に流れる電流の値 [A] を求める。

　バランサ接続前，負荷から電源に向かう中性線の電流は 30-20=10 A である。バランサを接続すると，中性線に流れる電流が 0 A となるような電流がバランサ側へ流れ込む。つまり，バランサの b-b’ に10 A の電流が流れる。
　バランサ b’-a’ に流れる電流を Ib’a’ ，b’-c’ に流れる電流を Ib’c’ とすると，バランサ内へは電流が均等に還流するので，

\(\ \ \ I_{b’a’}=I_{b’c’}\\ \ \ \ I_{b’a’}+I_{b’c’}=10\\ \ \ \ ∴I_{b’a’}=5\\ \)

　つまり，バランサ接続後 a’-b’ 間に流れる電流の値は 5 A となる。

(b) バランサ接続前後の線路損失の変化量の値 [W] を求める。

　バランサ接続前，電源から a 点の相に流れる電流は 30 A，中性線を通って負荷から電源に戻る電流は 10 A ， c 点の相を通って電源に向かう電流は 20 A となる。これら線路損失の合計は，

\(\ \ \ W_{b}=30^2\times0.1+10^2\times0.15+20^2\times0.1\\ \ \ \ \ \ =145[W]\\ \)

　バランサ接続後，電源から a 点の相に流れる電流は 30-5=25 A，中性線を通って負荷から電源に戻る電流は 0 A ， c 点の相を通って電源に向かう電流は 20+5=25 A となる。これら線路損失の合計は，

\(\ \ \ W_{a}=25^2\times0.1+0^2\times0.15+25^2\times0.1\\ \ \ \ \ \ =125[W]\\ \)

　バランサ接続前後の線路損失の変化量の値は，

\(\ \ \ W_{b}-W_a=145-125\\ \ \ \ \ \ =20[W]\\ \)

追加学習は配電の学習帳で

<<前問　　次問>>

電験３種の過去問一覧
電験記事一覧へもどる

電験３種過去問電力過去問, 電験3種, 電力, 配電, 2016年

Posted by ちゅん