解答
(a):（3）が最も近い。
(b):（4）が最も近い。
解説
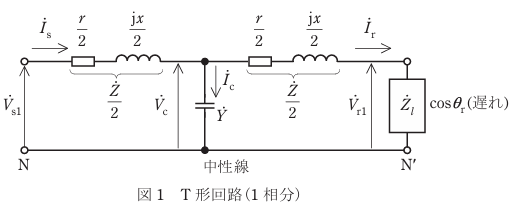
複素数によるベクトル計算を用いながら、計算をしていく必要があります。理論科目に近い計算量です。正答できる方は、是非ベクトル図も書いてみましょう。
(a) Vc[kV]を求める。
負荷電流 Ir を基準とすると、
\(\dot{V}_{r1}=V_{r1}cos\theta_r+jV_{r1}sin\theta_r\)
\(=150\times\frac{\sqrt3}{2}+j150\times\frac{1}{2}\)
\(=130+j75\)[kV]
負荷電流 Ir による電線路の電圧降下を VIr とすると、
\(\dot{V}_{I_r}=\dot{I}_r(\frac{r}{2}+j\frac{x}{2})V_{r1}\)
\(=400\times\frac{20}{2}+j400\times\frac{80}{2}\)
\(=4000+j16000\)[V]
\(=4+j16\)[kV]
したがって、
\(\dot{V}_{c}=\dot{V}_{r1}+\dot{V}_{I_r}\)
\(=130+j75+4+j16\)
\(=134+j91\)[kV]
\(V_{c}=\sqrt{134^2+91^2}=161.98\)[kV]
(b) Vs1[kV]を求める。
アドミタンスに流れる電流は、
\(\dot{I}_{c}=\dot{V}_c \dot{Y}\)
\(=(134000+j91000)\times j0.0007\)
\(=-63.7+j93.8\)[A]
したがって、
\(\dot{I}_{s}=\dot{I}_c +\dot{I}_r\)
\(=-63.7+j93.8+400=336.3+j93.8\)[A]
負荷電流 Is による電線路の電圧降下を VIs とすると、
\(\dot{V}_{I_s}=\dot{I}_{s}(\frac{r}{2}+j\frac{x}{2})V_{r1}\)
\(=(336.3+j93.8)(\frac{20}{2}+j\frac{80}{2})\)
\(=-389+j14390\)[V]
\(=-0.389+j14.39\)[kV]
よって
\(\dot{V}_{s1}=\dot{V}_{I_s}+\dot{V}_{c}\)
\(=-0.389+j14.39+134+j91\)
\(=133.611+j105.39\)[kV]
\(V_{c}=\sqrt{133.611^2+105.39^2}=170.17\)[kV]
