電験３種過去問【2020年機械 問17】

解答 

（a）の解答：（５）
（b）の解答：（４）

解説

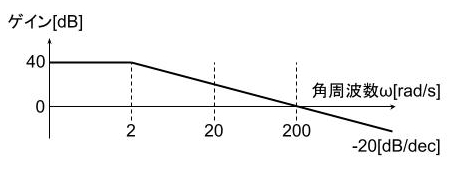
（a）図のボード線図から、比例要素と一次遅れ要素を直列接続したものと分かる。

したがって、周波数伝達関数G(jω)は

$\displaystyle G(j\omega)=k\times \frac{1}{1+j\omega T}$

また、ゲインgは次式で求められる。

$\displaystyle g=20\log_{10}|G(jω)|$[dB]

したがって、

ボード線図より、ω=0ではゲインg=40[dB]であるので

$\displaystyle 40=20\log_{10}k+20\log_{10}\left(\frac{1}{\sqrt{1+0^2}}\right)$

$\displaystyle 40=20\log_{10}k$

$\displaystyle 2=\log_{10}k$

$\displaystyle k=10^2=100$

また、ボード線図より、ω=200ではゲインg=0[dB]であるので

$\displaystyle 1+(200 T)^2=100^2$

$\displaystyle 1+40000 T^2=10000$

$\displaystyle T^2=\frac{10000-1}{40000}$

$\displaystyle T=0.499≒0.5$

よって、周波数伝達関数G(jω)は

$\displaystyle G(j \omega)=\frac{100}{1+j0.5\omega}$となる。

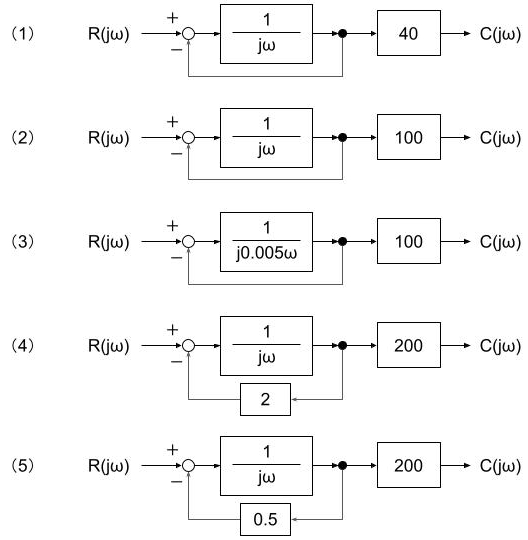
（b）回答中の周波数伝達関数G(s)のブロック線図はそれぞれ以下のようになる。

(1)

$\displaystyle G(s)=\frac{\frac{1}{j\omega}}{1+\left(\frac{1}{j\omega}\times1\right)}\times40$

$\displaystyle =\frac{1}{j\omega+1}\times40$

$\displaystyle =\frac{40}{1+j\omega}$

(2)

$\displaystyle G(s)=\frac{\frac{1}{j\omega}}{1+\left(\frac{1}{j\omega}\times1\right)}\times100$

$\displaystyle =\frac{1}{j\omega+1}\times100$

$\displaystyle =\frac{100}{1+j\omega}$

(3)

$\displaystyle G(s)=\frac{\frac{1}{j0.005\omega}}{1+\left(\frac{1}{j0.005\omega}\times1\right)}\times100$

$\displaystyle =\frac{1}{j0.005\omega+1}\times100$

$\displaystyle =\frac{100}{1+j0.005\omega}$

(4)

$\displaystyle G(s)=\frac{\frac{1}{j\omega}}{1+\left(\frac{1}{j\omega}\times2\right)}\times200$

$\displaystyle =\frac{1}{j\omega+2}\times200$

$\displaystyle =\frac{200}{2+j\omega}$

$\displaystyle =\frac{100}{1+j0.5\omega}$

(a)の解答と等しくなり、正しい。

(5)

$\displaystyle G(s)=\frac{\frac{1}{j\omega}}{1+\left(\frac{1}{j\omega}\times0.5\right)}\times200$

$\displaystyle =\frac{1}{j\omega+0.5}\times200$

$\displaystyle =\frac{200}{0.5+j\omega}$

$\displaystyle =\frac{400}{1+j2\omega}$