電験３種過去問【2018年機械 問3】

解答

（４）

解説

誘導電動機のトルクT[N・m]は、二次入力（同期ワット）P₂[W]に比例する。n_s[rpm]を誘導機電動機の同期速度とすると、トルクと二次入力の関係は次式となる。

$$T= \frac{60}{2 \pi n_s} P_{2}=KP_2　[W]$$

題意より、電源周波数は定格値で一定であるので、同期速度n_sは一定であり、トルクは二次入力に比例する。

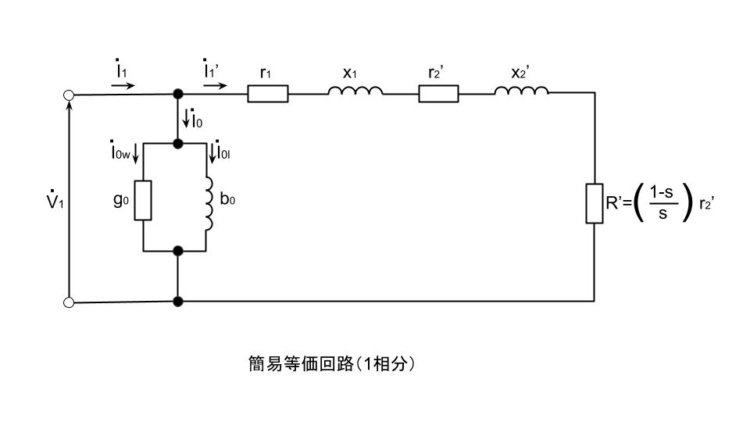
誘導電動機の1相分の簡易等価回路は上図のようになる。

簡易等価回路において、二次入力\(P_{2}=I_1’^2 \frac{r_2′}{s}[W]\)であたえられる。

定格電圧のときの二次入力\(P_{2(s=0.03)}=I_{1(s=0.03)}’^2 \frac{r_2′}{0.03}[W]\)

電源電圧が低下したときの二次入力\(P_{2(s=0.06)}=I_{1(s=0.06)}’^2 \frac{r_2′}{0.06}[W]\)

電源電圧が変化する前後で、負荷トルクが一定であるので、二次入力\(P_{2(s=0.03)}=P_{2(s=0.06)}\)である。

すなわち、$$I_{1(s=0.03)}’^2 \frac{r_2′}{0.03}=I_{1(s=0.06)}’^2 \frac{r_2′}{0.06}$$

$$ \left( \frac{I_{1(s=0.06)}’}{I_{1(s=0.03)}’} \right)^2= \frac{0.06}{0.03}=2$$

$$ \frac{I_{1(s=0.06)}’}{I_{1(s=0.03)}’}= \sqrt{2}=1.41$$

二次電流I₂と一次負荷電流I₁‘の関係は、一次巻線と二次巻線の巻き数比をαとするとI₁‘=I₂/αで与えられる。つまり一次負荷電流の比は、二次電流の比と等しいので、定格電圧での二次電流に対する電圧低下時の二次電流は1.41倍となる。