電験３種過去問【2017年電力 問8】

解答 

（２）

解説

電線の水平張力T[N]は次式で求められる。ここで、Ｓは電線の径間[m]、Dは電線の弛み[m]、Wは電線1ｍあたりの自重[N/m]。

\( \displaystyle T=\frac{WS^2}{8D}\)

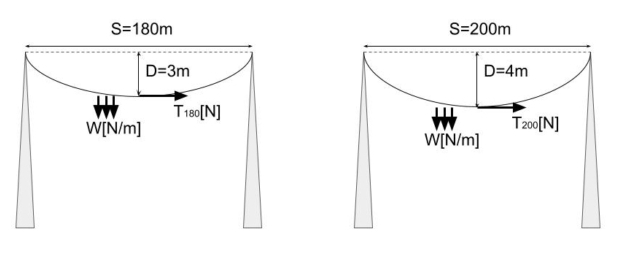
題意より、支持点間が180ｍ、たるみが3.0ｍのときの水平張力をT₁₈₀[N]とすると、

\( \displaystyle T_{180}=\frac{W \times 180^2}{8 \times 3}\)

\( \displaystyle W=\frac{24}{180^2} \times T_{180}\)　…（１）

支持点間が200ｍ、たるみが4.0ｍのときの水平張力をT₂₀₀[N]とすると、

\( \displaystyle T_{200}=\frac{W \times 200^2}{8 \times 4}\)

\( \displaystyle W=\frac{32}{200^2} \times T_{200}\)　…（２）

上式（１）と（２）をWについて整理すると、

\( \displaystyle \frac{24}{180^2}\times T_{180}=\frac{32}{200^2} \times T_{200}\)

\( \displaystyle T_{200}= \frac{24 \times200^2}{32 \times180^2} \times T_{180}=0.926\times T_{180}\)

すなわち、支持点間を200ｍにしたときの水平張力T₂₀₀[N]は、もとの水平張力T₁₈₀[N]の0.926倍（92.6％）となる。