電験２種過去問【2016年機械制御 問4】
【自動制御】現代制御、閉ループ状態方程式、定常偏差《計算問題》
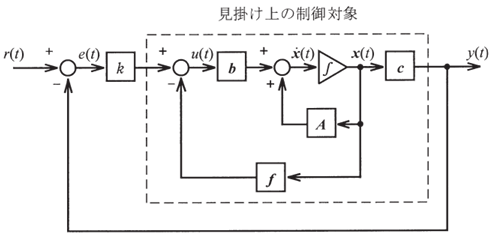
図に示す構造の制御系を考える。ここで r(t) は目標値、e(t) は制御偏差、u(t) は入力、x(t) は状態、y(t) は出力を表し、制御対象は次の状態方程式で記述される。
\(\boldsymbol{\dot{x}}(t)=\boldsymbol{Ax}(t)+\boldsymbol{b}u(t) \\y(t)=\boldsymbol{cx}(t)\) A=\(\begin{pmatrix}0&1\\0&-1\end{pmatrix}\),b=\(\begin{pmatrix}0\\1\end{pmatrix}\),c=\(\begin{pmatrix}0&1\end{pmatrix}\)次の問に答えよ。
解答と解説はこちら
解答
公式標準解答
解説
現代制御からの出題です。２種では古典制御からの出題がほとんどですが、このように稀に現代制御からも出題があります。捻った問題ではないので、解き方を理解していれば簡単な部類となります。しかし、計算が複雑で問題を選択するかどうかは一考の余地ありです。
今後も現代制御から出題されることもあると思いますので、余裕があれば取り組んでおきたいところです。
標準解答の補足
(4)下のように定まるので、x(∞)を導出できる。
\(\boldsymbol{\dot{x}}(∞)\)= \(\begin{pmatrix}0\\0\end{pmatrix}\)なので \(\begin{pmatrix}0&1\\-12-2k&-7-k\end{pmatrix}\)x(∞)=-\(\begin{pmatrix}0\\1\end{pmatrix}\)kr₀ \(\begin{pmatrix}0&1\\-12-2k&-7-k\end{pmatrix}\)の逆行列を両辺にかけると標準解答のようになる。
追加学習は自動制御の学習帳で