電験２種過去問【2021年電力管理 問3】

解答

（１）線間電圧154kV、三相容量100MV・Aを基準値とするとき、次を求めよ。
　a）基準電流\(I_B\)[kA] 
　\(\displaystyle I_B=\frac{100\times10^6}{\sqrt3\times154\times10^3}=375\)[A]　\(\displaystyle I_B=0.375\)[kA] 

　b）基準インピーダンス\(Z_B\)[Ω] 
　\(\displaystyle Z_B=\frac{\frac{154\times10^3}{\sqrt3}}{375}=237\)[Ω]

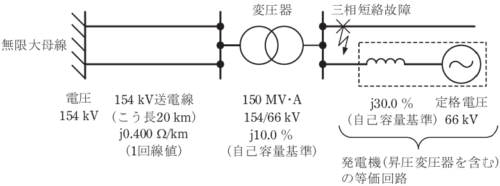
（２）図に示す無限大母線と送電線、変圧器、発電機から構成される電力系統を対象として、以下の量を、100MV・Aを基準容量とし各部の公称電圧ないしは定格電圧を基準電圧とする単位法による値に換算せよ。
　a）公称電圧154kVのこう長20kmの１回線送電線のインピーダンスを上記の単位法の値[p.u.]に換算せよ。ただし、送電線（１回線）のインピーダンスはj0.400Ω/kmとする。
　\(\displaystyle Z=\frac{j0.400\times20}{237}=j0.0337\)[p.u.] 

　b）容量150MV・Aの変圧器(154/66kV)のインピーダンスを上記の単位法の値[p.u.]に換算せよ。ただし、同変圧器のインピーダンスは自己容量基準でj10.0%とする。
　\(\displaystyle Z=\frac{j10.0}{100}\times\frac{100}{150}=j0.0667\)[p.u.] 

　c）変圧器二次側(定格電圧66kV)の電流25kAを上記の単位法の値[p.u.]に換算せよ。
　154ｋV基準電流値\(I_B=375\)[A]を二次側66ｋVへ換算すれば、
　\(\displaystyle I_B’=375\times\frac{154}{66}=875\)[A] であるので
　\(\displaystyle I=\frac{25\times10^3}{875}=28.6\)[p.u.] 

（３）図の電力系統で、変圧器二次側(定格電圧66kV)の母線至近端での三相短絡時における故障電流を25kA以下に抑えることができる発電機の最大容量S[MV・A]を求めよ。ここに送電線と変圧器のインピーダンスは小問（2）に示すとおりであるが、154kV送電線は2回線とする。また発電機(昇圧変圧器を含む)は、定格電圧が66kVの電圧源と自己容量基準でj30.0%のインピーダンスの直列回路で表すこととする。なお無限大母線の電圧は154kV、電圧源の電圧は66kVとする。

　こう長分の単位法によるインピーダンス\(Z_L\)（100MV・A基準）は、2回線あるので
　\(\displaystyle Z_L=\frac{j0.0337}{2}=j0.0169\)[p.u.] 

　変圧器分の単位法によるインピーダンス\(Z_T\)（100MV・A基準）は、前問より
　\(\displaystyle Z_T=j0.0667\)[p.u.] 
　
　無限大母線側からの三相短絡故障電流\(I_{sL}\)は
　\(\displaystyle I_{sL}=\frac{I_B’}{Z_L+Z_T}\)
　\(\displaystyle 　=\frac{I_B’}{j0.0169+j0.0667}=\frac{I_B’}{j0.0836}\)[A] 

　発電機分の単位法によるインピーダンス\(Z_G\)（100MV・A基準）は、
　\(\displaystyle Z_G=\frac{j30}{100}\times\frac{100}{S}=\frac{j30}{S}\)[p.u.] 

　発電機からの三相短絡故障電流\(I_{sG}\)は
　\(\displaystyle I_{sG}=\frac{I_B’}{Z_G}\)
　\(\displaystyle 　=\frac{I_B’}{\frac{j30}{S}}\)[A] 

　三相短絡故障電流\(I_{s}\)は
　\(\displaystyle I_{s}=I_{sL}+I_{sG}\)
　\(\displaystyle 　=I_B'(\frac{1}{j0.0836}+\frac{1}{\frac{j30}{S}})\)
　\(\displaystyle 　=I_B'(-j12.0-j0.0333S)\)
　\(\displaystyle 　=-j(12.0+0.0333S)I_B’\)[A] 

　一方で、変圧器二次側(定格電圧66kV)の電流25kAの単位法の値は28.6[p.u.]であったので、
　\(\displaystyle 25\times10^3=28.6I_B’\)[A] であったので
　\(\displaystyle 12.0+0.0333S=28.6\)
　であるときに、三相短絡故障電流\(I_{s}\)は25kA流れる。

　つまり、
　\(\displaystyle 0.0333S=16.6\)
　\(\displaystyle S=498\)[MV・A]が最大容量である。

解説

なし