電験3種過去問【2019年機械 問5】
【同期機】三相同期電動機の入出力とトルク《空所問題》
次の文章は、星形結線の円筒形三相同期電動機の入力、出力、トルクに関する記述である。
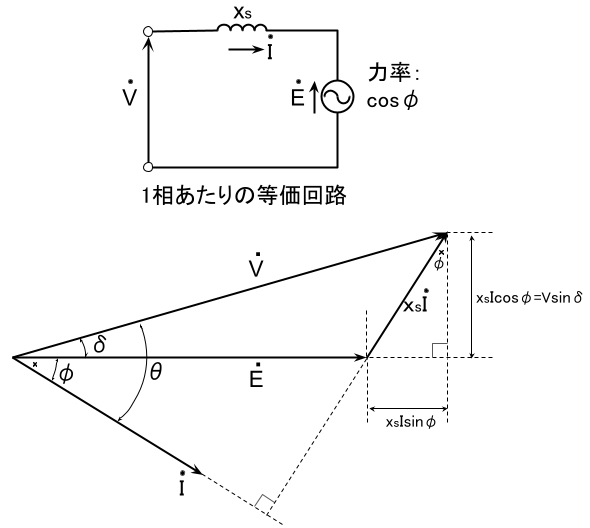
この三相同期電動機の1相分の誘導起電力\(E\)[V]、電圧\(V\)[V]、電流\(I\)[A]、\(V\)と\(I\)の位相差を\(\theta\)[rad]としたときの1相分の入力\(P_i\)[W]は次式で表される。
$$P_i=VI\cos\theta$$
また、\(E\)と\(V\)の位相差を\(\delta\)[rad]とすると、1相分の出力\(P_o\)[W]は次式で表される。\(E\)と\(V\)の位相差\(\delta\)は\(\fbox{(ア)}\)といわれる。
$$P_o=EI\cos(\delta-\theta)=\frac{VE}{x}\fbox{(イ)}$$
ここで\(x\)[Ω]は同期リアクタンスであり、電機子巻線抵抗は無視できるものとする。
この三相同期電動機の全出力を\(P\)[W]、同期速度を\(n_s\)[min-1]とすると、トルク\(T\)[N・m]とPの関係は次式で表される。
$$P=3P_o=2\pi\frac{n_s}{60}T$$
これから、\(T\)は次式のようになる。
$$T=\frac{60}{2\pi n_s}・3P_o=\frac{60}{2\pi n_s}・\frac{3VE}{x}\fbox{(イ)}$$
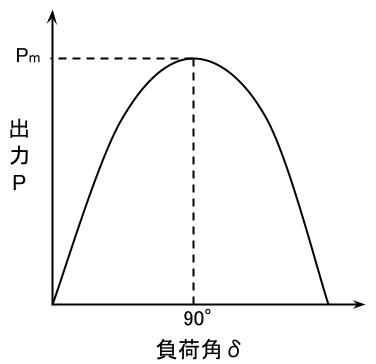
以上のことから、\(\displaystyle 0≦\delta≦\frac{\pi}{2}\)の範囲において\(\delta\)が\(\fbox{(ウ)}\)なるに従って\(T\)は\(\fbox{(エ)}\)なり、理論上\(\displaystyle \frac{\pi}{2}\)[rad]のとき\(\fbox{(オ)}\)となる。
上記の記述中の空白箇所(ア)~(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

ディスカッション
コメント一覧
まだ、コメントがありません