電験3種過去問【2022年(下期)電力 問9】
【送電】受電端負荷の有効電力計算《計算問題》
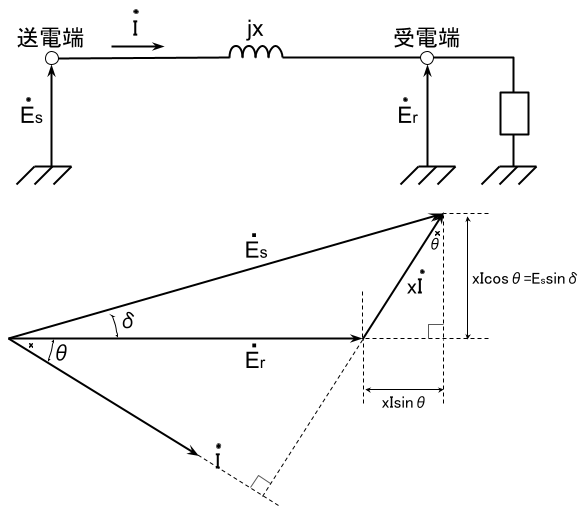
交流三相3線式1回線の送電線路があり、受電端に遅れ力率\(\theta\)[rad]の負荷が接続されている。送電端の線間電圧を\(V_s\)[V]、受電端の線間電圧を\(V_r\)[V]、その間の位相差角は\(\delta\)[rad]である。
受電端の負荷に供給されている三相有効電力[W]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、送電端と受電端の間における電線1線当たりの誘導性リアクタンスはX[Ω]とし、線路の抵抗、静電容量は無視するものとする。
\(\small{\begin{array}{cccc}
&(1)\displaystyle\frac{V_sV_r}{X}\sin\delta&(2)\displaystyle\frac{\sqrt3V_sV_r}{X}\cos\theta&(3)\displaystyle\frac{\sqrt3V_sV_r}{X}\sin\delta&(4)\displaystyle\frac{V_sV_r}{X}\cos\delta&(5)\displaystyle\frac{V_sV_r}{X\sin\delta}\cos\theta\\
\end{array}}\)

ディスカッション
コメント一覧
まだ、コメントがありません