解答
(a):（5）が最も近い。
(b):（1）が最も近い。
解説
ケーブルの静電容量についてしっかり理解しておく必要があります。
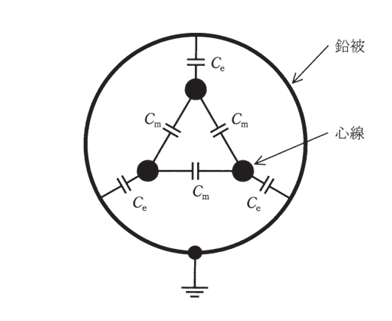
(a) 対地静電容量 Ce [F] と線間静電容量 Cm [F] の比\(\frac{C_e}{C_m}\)を求める。
受電端を開放した状態で，送電端で三つの心線を一括してこれと大地間に\(\frac{E}{\sqrt3}\) [V] の交流電圧を加えたとき，全充電電流は 90 A であった。心線を一括しているので線間静電容量 Cm [F] は短絡されている状態である。つまり，このときの対地静電容量は 3Ce [F] となる。したがって，角周波数を ω [rad/s] とすると，次式が成立する。
\(\frac{\frac{E}{\sqrt3}}{\frac{1}{\omega 3C_e}}=90\)
∴\(\sqrt3E\omega C_e=90\)
∴\(C_e=\frac{90}{\sqrt3E\omega}\)…➀
二つの心線の受電端・送電端を接地し，受電端を開放した残りの心線と大地間に\(\frac{E}{\sqrt3}\) [V] の交流電圧を送電端に加えたとき，心線に流れる充電電流は 45 A であった。二つの心線の受電端・送電端を接地しているので，この二つの心線間の Cm [F] と，二つそれぞれの Ce [F] は短絡されている状態である。このときの，残りの心線と大地間の対地静電容量は 2Cm+Ce [F] となる。したがって，
\(\frac{\frac{E}{\sqrt3}}{\frac{1}{\omega (2C_m+C_e)}}=45\)
∴\(\frac{E\omega (2C_m+C_e)}{\sqrt3}=45\)
∴\(2C_m+C_e=\frac{45\sqrt3}{E\omega}\)
➀を代入して
∴\(2C_m=\frac{45\sqrt3}{E\omega}-\frac{90}{\sqrt3E\omega}\)
∴\(2C_m=\frac{3\times45-90}{\sqrt3E\omega}\)
∴\(C_m=\frac{22.5}{\sqrt3E\omega}\)…②
➀，②より
\(\frac{C_e}{C_m}=\frac{90}{22.5}=4\)…③
(b) 1 線に流れる充電電流の値 [A]を求める。
Δ回路に全て同じ平衡負荷抵抗RΔ[Ω]が接続されているとき、これをY回路に変換したときの1相の平衡負荷RY[Ω]は、
\(\displaystyle R_Y=\frac{R_Δ}{3}\)[Ω]
Δ回路に平衡インピーダンス\(\frac{1}{\omega C_m}\)[Ω]が接続されているとき、これをY回路に変換したときの1相の平衡インピーダンスは
\(\frac{\frac{1}{\omega C_m}}{3}\)
\(=\frac{1}{\omega 3C_m}\)[Ω]
以上より，Δ接続されている静電容量 Cm [F] は，Y回路に変換すると1相分の静電容量は 3Cm [F] となる。
線間静電容量 Cm [F] を，対地静電容量に置き換えると 3Cm [F]であるので，1相分の対地静電容量は
\(C_e+3C_m\)[F]
定格三相電圧では，1 相にかかる電圧は\(\frac{E}{\sqrt3}\) [V]である。つまり，1 線に流れる電流は
\(I=\frac{\frac{E}{\sqrt3}}{\frac{1}{\omega (C_e+3C_m)}}\)[A]
前問③より Ce=4Cm なので，
\(I=\frac{7E\omega C_m}{\sqrt3}\)
②を代入して，
\(I=\frac{7E\omega \frac{22.5}{\sqrt3E\omega}}{\sqrt3}\)
\(=\frac{7 \times22.5}{3}=52.5\)[A]
