解答
(a):(2)が最も近い。
(b):(3)が最も近い。
解説
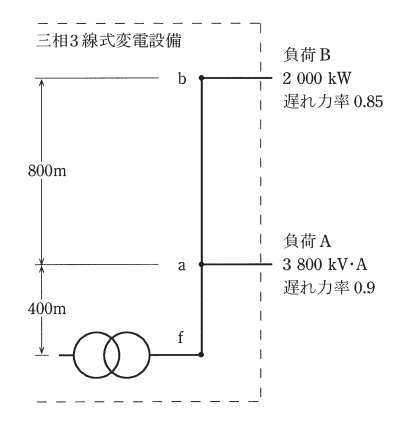
分岐点での合成電力を求める計算の難易度は高くありません。しかし(b)問題の計算量は非常に多くかなり複雑です。
(a) 負荷 A と負荷 B で消費される無効電力の合計値 [kvar] を求める。
負荷 A の力率は cosθA=0.9 ,負荷 B の力率は cosθB=0.85 であるので,
\(\ \ \ \sin\theta_A=\sqrt{1^2-\cos\theta_A^2}=0.436\\
\ \ \ \sin\theta_B=\sqrt{1^2-\cos\theta_B^2}=0.527\\
\)
負荷 A と負荷 B で消費される無効電力の合計値 [kvar] は,
\(\ \ \ Q_A+Q_B=3800\sin\theta_A+2000\tan\theta_B\\
\ \ \ \ \ \ =3800\times0.436+2000\frac{0.527}{0.85}\\
\ \ \ \ \ \ =2896.8[kvar]\\
\)
となる。
(b) f-b 間の線間電圧の電圧降下 Vfb の値 [V] を求める。
f-a 間の抵抗 rfa [Ω],リアクタンス xfa [Ω]および,a-b 間の抵抗 rab [Ω],リアクタンス xab [Ω]は,
\(\ \ \ r_{fa}=0.24\times\frac{400}{1000}=0.096\\
\ \ \ x_{fa}=0.18\times\frac{400}{1000}=0.072\\
\ \ \ r_{ab}=0.24\times\frac{800}{1000}=0.192\\
\ \ \ x_{ab}=0.18\times\frac{800}{1000}=0.144\\
\)
ここで,電圧降下等価抵抗は\(\displaystyle Z=r\cos\theta+x\sin\theta\) [Ω]で与えられ,cosθ は負荷の力率である。
a 点の力率は負荷 A と負荷 B で消費される電力の合計となる。a 点での有効電力,無効電力および力率は,
\(\ \ \ P_a=3800\cos\theta_A+2000\\
\ \ \ \ \ =5420[kW]\\
\ \ \ Q_a=Q_A+Q_B\\
\ \ \ \ \ =2896.8[kvar]\\
\ \ \ \cos\theta_a=\frac{P_a}{\sqrt{P_a^2+Q_a^2}}\\
\ \ \ \ \ =0.882\\
\ \ \ \sin\theta_a=\frac{Q_a}{\sqrt{P_a^2+Q_a^2}}\\
\ \ \ \ \ =0.471\\
\)
f-a 間の電圧降下等価抵抗 Zfa [Ω] および,a-b 間の電圧降下等価抵抗 Zab [Ω]は,
\(\ \ \ Z_{fa}=r_{fa}\cos\theta_a+x_{fa}\sin\theta_a\\
\ \ \ \ \ =0.118584\\
\ \ \ Z_{ab}=r_{ab}\cos\theta_B+x_{ab}\sin\theta_B\\
\ \ \ \ \ =0.239088\\
\)
a-b 間を流れる電流 Iab および,a-b 間の線路 1 線当たりの電圧降下 Eab は,
\(\ \ \ I_{ab}=\frac{2000\times10^3}{\sqrt3\times22\times10^3\cos\theta_B}\\
\ \ \ \ \ =61.75[A]\\
\ \ \ E_{ab}=I_{ab}Z_{ab}\\
\ \ \ \ \ =14.76[V]\\
\)
a-b 間の線路 1 線当たりの電圧降下 Eab は線路 1 線当たりの電圧降下であり相電圧に相当するので,a 点の電圧値は
\(\ \ \ V_{a}=22\times10^3+\sqrt3E_{ab}\\
\ \ \ \ \ =22026[V]\\
\)
f-a 間を流れる電流 Ifa および,f-a 間の線路 1 線当たりの電圧降下 Efa は,
\(\ \ \ I_{fa}=\frac{P_a\times10^3}{\sqrt3V_a\cos\theta_a}\\
\ \ \ \ \ =\frac{5420\times10^3}{\sqrt3\times22.026\times10^3\times0.882\\
\ \ \ \ \ =161.1[A]\\
\ \ \ E_{fa}=I_{fa}Z_{fa}\\
\ \ \ \ \ =19.1[V]\\
\)
f-b 間の線間電圧の電圧降下 Vfb の値は,
\(\ \ \ V_{fa}=\sqrt3(E_{ab}+E_{fb})\\
\ \ \ \ \ =58.7[V]\\
\)

ディスカッション
コメント一覧
まだ、コメントがありません