Loading [MathJax]/jax/element/mml/optable/GreekAndCoptic.js
// google adsence用 電験２種過去問【2021年理論 問1】 | 電気主任技術者のいろは

電験２種過去問【2021年理論 問1】

2022年4月24日

【電磁気】二種類の誘電体を有する平行平板コンデンサ《空所問題》

　次の文章は、平行平板コンデンサに関する記述である。文中の\fbox{空所欄}に当てはまる最も適切なものを解答群の中から選べ。
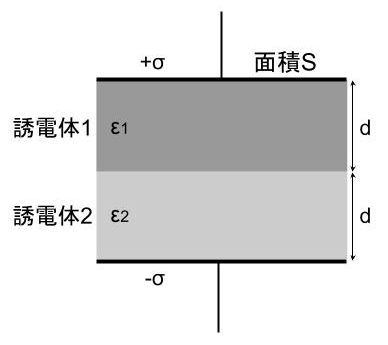
　図のように、平行平板コンデンサの極板間に二種類の誘電体１、誘電体２が挿入されている。各誘電体の誘電率はε1、ε2であり、厚さはともにdである。極板の面積はSであり、端効果は無視できるものとする。
　コンデンサの極板間には直流電圧が印加されており、各極板に単位面積当たり±σの電荷が図に示すように現れている。このときの誘電体１中の電束密度の大きさは\fbox{（１）}、電界の大きさは\fbox{（２）}と表される。同様に誘電他２中の電界の大きさを求めると、コンデンサの極板間に印加された電圧は\fbox{（３）}と表すことがきる。
　コンデンサ全体に蓄えられた電界のエネルギーは\fbox{（４）}と表される。誘電体１の領域に蓄えられた電界のエネルギーが誘電体２の領域に蓄えられた電界のエネルギーよりも大きい場合、誘電率ε1とε2との間には\fbox{（５）}の関係が成立する。

［問１の解答群］

(ｲ) \displaystyle \frac{ε_{1}σ}{ε_{1}+ε_{2}}　(ﾛ) \displaystyle \frac{(ε_{1}+ε_{2})σd}{ε_{1}ε_{2}}　(ﾊ) \displaystyle \frac{σ}{ε_{1}}　(ﾆ) \displaystyle ε_{1}>ε_{2}

(ﾎ) \displaystyle ε_{1}ε_{2}=0　(ﾍ) \displaystyle ε_{1}<ε_{2}　(ﾄ) \displaystyle \frac{σ}{ε_{1}+ε_{2}}　(ﾁ) \displaystyle \frac{(ε_{1}+ε_{2})σ^2S}{2d}

(ﾘ) \displaystyle \frac{ε_{1}ε_{2}σd}{ε_{1}+ε_{2}}　(ﾇ) \displaystyle \frac{(ε_{1}+ε_{2})σ^2dS}{2ε_{1}ε_{2}}　(ﾙ) \displaystyle 2σ　(ｦ) \displaystyle \frac{(ε_{1}+ε_{2})σ}{d}

(ﾜ) \displaystyle \frac{ε_{1}ε_{2}σ^2dS}{2(ε_{1}+ε_{2})}　(ｶ) \displaystyle σ　(ﾖ) \displaystyle ε_{1}σ

解答と解説はこちら

解答

(１)：（カ）
(２)：（ハ）
(３)：（ロ）
(４)：（ヌ）
(５)：（ヘ）

解説

Q[C]の電荷から、Q[C]の電束が発生する。単位面積当たりの電束が電束密度Dであるので、

単位面積当たり±σの電荷が現れているときの誘電体１中の電束密度Dの大きさは\displaystyle σ 、電界の大きさは\displaystyle E_1=\frac{D}{ε_1}=\frac{σ}{ε_1}と表される。

同様に誘電他２中の電界の大きさを求めると、\displaystyle E_2=\frac{σ}{ε_2}と表される。

コンデンサの極板間に印加された電圧は

\displaystyle V=V_1+V_2=E_1d+E_2d

\displaystyle =\frac{σd}{ε_1}+\frac{σd}{ε_2}=\frac{(ε_{1}+ε_{2})σd}{ε_{1}ε_{2}}

と表すことがきる。

コンデンサ全体に蓄えられた電界のエネルギーは

\displaystyle W=\frac{1}{2}CV^2=\frac{1}{2}QV=\frac{1}{2}σSV

\displaystyle =\frac{1}{2}σS\frac{(ε_{1}+ε_{2})σd}{ε_{1}ε_{2}}=\frac{(ε_{1}+ε_{2})σ^2dS}{2ε_{1}ε_{2}}

と表される。

誘電体１の領域に蓄えられた電界のエネルギーは

\displaystyle W_1=\frac{1}{2}σSV_1=\frac{1}{2}σSE_1d=\frac{1}{2}σS\frac{σ}{ε_1}d=\frac{σ^2dS}{2ε_1}

誘電体２の領域に蓄えられた電界のエネルギーは

\displaystyle W_2=\frac{1}{2}σSV_2=\frac{1}{2}σSE_2d=\frac{1}{2}σS\frac{σ}{ε_2}d=\frac{σ^2dS}{2ε_2}

\displaystyle W_1が \displaystyle W_2よりも大きい場合、

誘電率ε1とε2との間には \displaystyle ε_{1}<ε_{2}の関係が成立する。

<<前問　　次問>>

 

電験２種過去問理論過去問, 電験2種, 理論, 電磁気, 2021年

Posted by ちゅん