電験2種過去問【2023年機械制御 問4】
【自動制御】古典制御、ゲイン特性、折れ線近似《計算問題》
本問題で扱う伝達関数の全ての極と零点は複素平面上の右半平面には存在しないものと仮定する。以下の問に答えよ。ここで必要に応じて、14=20log₁₀100.7、100.7=5.0119を用いよ。ただし、全ての図は折れ線近似で表している。
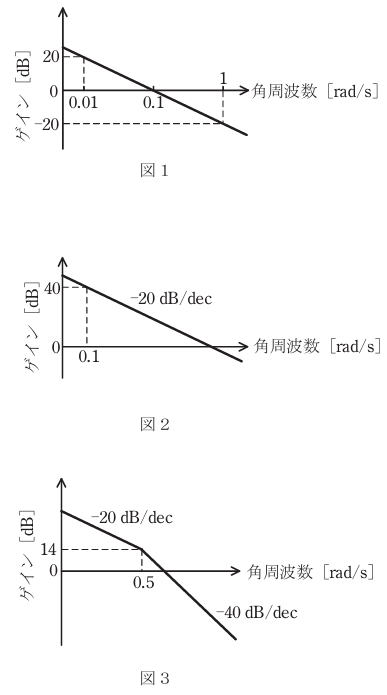
(1)図1に示すゲイン特性曲線から積分要素の伝達関数 G₁(s)=\(\frac{1}{T_{I}s}\)を求めよ。
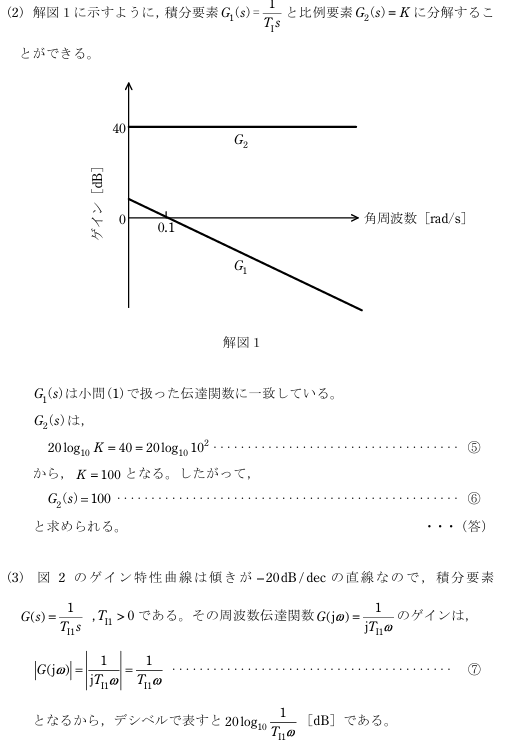
(2)図2に示すゲイン特性曲線が表す伝達関数 G(s) を G(s)=G₁(s)G₂(s) のように分解して考える。G₁(s) を小問(1)で求めた伝達関数とするときの G₂(s) を求めよ。
(3)図2に示すゲイン特性曲線から伝達関数 G(s) を求めよ。ただし、 G(s)=\(\frac{1}{T_{I1}s}\) とおいて、その周波数伝達関数 G(s)=\(\frac{1}{jT_{I}ω}\) のゲインが ω=0.1 rad/s のとき 40 dB であることを用いて TI1 を決定せよ。
(4)折れ線近似で表した図3に示すゲイン特性曲線から伝達関数 G(s) を求めよ。ただし、 G(s) を積分要素 G₁(s)=\(\frac{1}{T_{I2}s}\) と一次遅れ要素 G₂(s)=\(\frac{1}{1+Ts}\) に分関して考えよ。
追加学習は自動制御の学習帳で


ディスカッション
コメント一覧
まだ、コメントがありません