電験２種過去問【2021年機械 問4】

解答

(１)：（ヌ）
(２)：（ヘ）
(３)：（カ）
(４)：（ホ）
(５)：（ワ）

解説

　変圧器の一次巻線と二次巻線とを別々の巻線にしないで、一次巻線と二次巻線の一部を共用して使用する変圧器を$\fbox{単巻変圧器}$といい、この変圧器の一次、二次に共通した巻線を$\fbox{分路巻線}$、共通でない部分を$\fbox{直列巻線}$という。
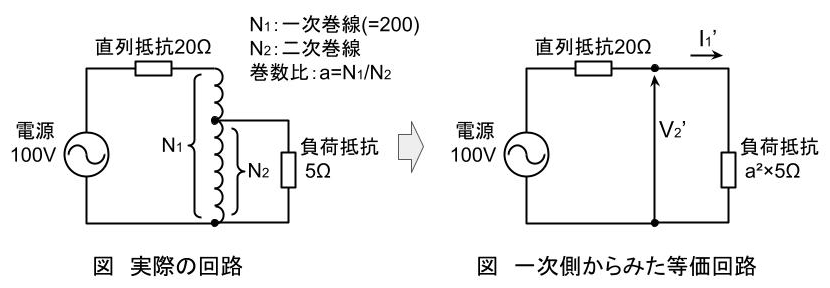
　図に示すように$\fbox{単巻変圧器}$の一次側に20Ωの直列抵抗、二次側に5Ωの負荷抵抗を接続し、電源電圧を100Vとする。一次巻線の巻数を$\displaystyle N_1=200$とした場合に、5Ωの負荷抵抗で消費される電力が最大となる二次巻数は$\displaystyle N_2=$$\fbox{100}$となり、このときの負荷抵抗の消費電力は$\fbox{125}$Wとなる。なお変圧器は理想変圧器として考える。

　変圧器の一次側換算した、二次側負荷抵抗$\displaystyle R_L’$は、二次側負荷抵抗を$\displaystyle R_L$とすると、

$\displaystyle R_L’＝a^2R_L$

したがって、一次側からみた等価回路は上図のようになる。

負荷抵抗$\displaystyle R_L’$で消費される抵抗が最大となる条件は、

$\displaystyle 5a^2=20$　※電験３種過去問【2021年理論 問7】（最大消費電力の条件）

$\displaystyle a=\sqrt{\frac{20}{5}}=\frac{N_1}{N_2}=\frac{200}{N_2}$

$\displaystyle N_2=\frac{200}{\sqrt{4}}=100$

つまり、$\displaystyle N_2=100$のとき、負荷抵抗$\displaystyle R_L’$で消費される抵抗が最大となる。

$\displaystyle a=\frac{N_1}{N_2}=2$となったときの、負荷抵抗での消費電力(=$\displaystyle R_L’$での消費電力)$\displaystyle P_L$は

$\displaystyle P_L＝\frac{V_2’^2}{5a^2}=\frac{\left(100\times\frac{5a^2}{20+5a^2}\right)^2}{5a^2}$

$\displaystyle ＝\frac{50^2}{20}=125\text{[W]}$

負荷抵抗での消費電力は$\displaystyle P_L’=125\text{[W]}$となる。