電験２種過去問【2018年機械 問1】

解答

解説

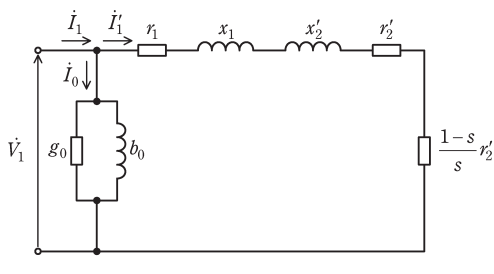
　図は、三相誘導電動機の1相分のL形等価回路である。ただし、\(r_1\)は一次巻線抵抗、\(r_2’\)は二次巻線抵抗の一次換算値、\(x_1\)は一次漏れリアクタンス、\(x_2’\)は二次漏れリアクタンスの一次換算値、\(b_0及びg_0\)は励磁サセプタンス及び励磁コンダクタンスである。三相交流電源の相電圧の実効値を\(V_1\)、フェーザを\(\dot{V_1}\)とする。また、滑りを\(s\)とし、漏れリアクタンスの和を\(X=x_1+x_2’\)とする。
　電動機を交流電源に接続すると、励磁電流は\(\dot{I_0}=\dot{Y}\dot{V_1}\)となり、アドミタンス\(\dot{Y}=g_0-jb_0\)であるので

\(\dot{I_0}=(ﾙ)(g_0-jb_0)\dot{V_1}\)となる。

　\(\dot{I_0}\)による損失は\(g_0\)を流れる電流となるので

\(W_I=(ｦ)3g_0V_1^2\)である。

機械損\(W_m\)を無視すると、機械的出力は\(P_O=\displaystyle 3I_1’^2\frac{1-s}{s}r_2’\)である。

ここで、

\(\displaystyle I_1’=\frac{V_1}{\sqrt{\left(r_1+r_2’+\frac{1-s}{s}r_2’\right)^2+\left(x_1+x_2’\right)^2}}\)

\(\displaystyle =\frac{V_1}{\sqrt{\left(r_1+\frac{r_2′}{s}\right)^2+X^2}}\)

であるので、

\(P_O=(ﾛ)\displaystyle\frac{3\frac{1-s}{s}r_2’V_1^2}{\left(r_1+\frac{r_2′}{s}\right)^2+X^2}\)である。

 一方、\(r_1及びr_2’\)に生じる損失は\(W_C=3I_1’^2(r_1+r_2′)\)であるので、

\(W_C=(ﾁ)\displaystyle\frac{3(r_1+r_2′)V_1^2}{\left(r_1+\frac{r_2′}{s}\right)^2+X^2}\)となる。

ここで、機械損\(W_m\)を考慮すると、電動機の効率は\((ｲ)\displaystyle\frac{P_O-W_m}{P_O+W_I+W_C}\)となる。