電験１種過去問【2014年電力管理問3】

2014年12月1日2024年4月14日

【送電】対象座標法を用いた送電線の１線断線故障相電圧計算《計算問題》

　図１は１回線送電線を介して同期発電機、昇圧変圧器から三相平衡負荷へ送電している状況を示す。１線断線故障に関して、次の問に答えよ。ただし、送電線の作用静電容量は無視できるものとし、数値は全て 100 MV・A 基準の単位法で表現するものとする。

　図１の送電線の送電端（昇圧変圧器高圧側母線 S）近傍で１線断線が発生した回路の対称分等価回路を導出するために、図２のように元の系統を断線事故発生地点で二分割する。１線断線故障が発生したとき、図２の$\dot{I}_{1a},\dot{I}_{1b},\dot{I}_{1c},\dot{I}_{2a},\dot{I}_{2b},\dot{I}_{2c},$$\dot{V}_{1a},\dot{V}_{1b},\dot{V}_{1c},\dot{V}_{2a},\dot{V}_{2b},\dot{V}_{2c}$の間に成立する関係式（１線断線条件）を示せ。ただし、断線事故が発生した相を a 相とすること。
　上記 1. で得られた関係式を対象座標変換すると１線断線条件が得られる。これを表現する図３の対称分等価回路の各$\fbox{$\phantom{四角空所}$}$に入るべき数値をそれぞれ答えよ。ただし、同じ文字をもつ$\fbox{$\phantom{四角空所}$}$には同じ数値が入る。負荷を除く各回路要素のインピーダンスは全て [p.u.] で表現すること。
　事故発生前の送電端（母線 S）電圧を 1.0 p.u. ここからの送電電力を 90 MW +j10 Mvar とする。以下の各問に答えよ。
ａ.　事故発生前の発電機内部電圧（図１に示した発電機正相リアクタンス背後電圧）の大きさを計算せよ。
ｂ.　１線断線直後には発電機内部電圧（正相リアクタンス背後電圧）が変化しないものとして、事故発生直後の系統状態を図４で表現したときの電流$\dot{I}_{p}$を計算せよ。ただし、発電機内部電圧の位相を基準にすること。
ｃ.　１線断線直後の母線 S の事故相電圧の大きさを計算せよ。

解答と解説はこちら

解答

公式標準解答(※太字は補足)

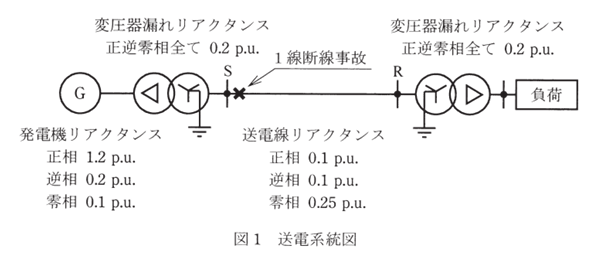
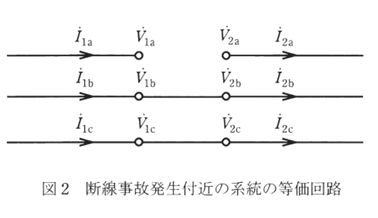
1. 　図１の送電線の送電端（昇圧変圧器高圧側母線 S）近傍で１線断線が発生した回路の対称分等価回路を導出するために、図２のように元の系統を断線事故発生地点で二分割する。１線断線故障が発生したとき、図２の$\dot{I}_{1a},\dot{I}_{1b},\dot{I}_{1c},\dot{I}_{2a},\dot{I}_{2b},\dot{I}_{2c},$$\dot{V}_{1a},\dot{V}_{1b},\dot{V}_{1c},\dot{V}_{2a},\dot{V}_{2b},\dot{V}_{2c}$の間に成立する関係式（１線断線条件）を示せ。ただし、断線事故が発生した相を a 相とすること。

　a 相は断線、それ以外は健全（接続）という条件なので、求める条件は以下のとおりである。

$\left. \begin{array}{l} \dot{I}_{1a}=\dot{I}_{2a}=0\\ \dot{I}_{1b}=\dot{I}_{2b}\\ \dot{I}_{1c}=\dot{I}_{2c}\\ \dot{V}_{1b}=\dot{V}_{2b}\\ \dot{V}_{1c}=\dot{V}_{2c} \end{array} \right\}$…(答)

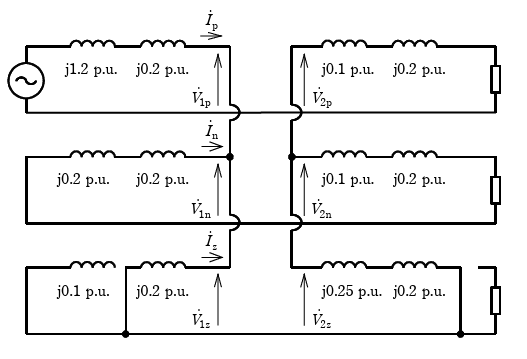
2.　上記 1. で得られた関係式を対象座標変換すると１線断線条件が得られる。これを表現する図３の対称分等価回路の各$\fbox{$\phantom{四角空所}$}$に入るべき数値をそれぞれ答えよ。ただし、同じ文字をもつ$\fbox{$\phantom{四角空所}$}$には同じ数値が入る。負荷を除く各回路要素のインピーダンスは全て [p.u.] で表現すること。

　１線断線の対称分等価回路を書けば次のようになる。（負荷インピーダンスと電源電圧の値は 3. で与えられるので、ここでは記入しなくてよい。）

したがって、

$\left. \begin{array}{l} a=j1.2p.u.,b=j0.2p.u.,\\ c=j0.1p.u.,d=j0.2p.u,\\ e=j0.1p.u.,f=j0.25p.u.,\\ g=j0.2p.u. \end{array} \right\}$…(答)

3.　事故発生前の送電端（母線 S）電圧を 1.0 p.u. ここからの送電電力を 90 MW +j10 Mvar とする。以下の各問に答えよ。
ａ.　事故発生前の発電機内部電圧（図１に示した発電機正相リアクタンス背後電圧）の大きさを計算せよ。
ｂ.　１線断線直後には発電機内部電圧（正相リアクタンス背後電圧）が変化しないものとして、事故発生直後の系統状態を図４で表現したときの電流$\dot{I}_{p}$を計算せよ。ただし、発電機内部電圧の位相を基準にすること。
ｃ.　１線断線直後の母線 S の事故相電圧の大きさを計算せよ。

a.　題意より送電端（電圧$\dot{V}_1$）から負荷側を見た等価インピーダンス$\dot{Z}_1$は、
　$\dot{Z_1}=\frac{\dot{V_1}}{\dot{I}}=\frac{1}{0.9-j0.1}$=1.0976+j0.12195 p.u.
である。したがって負荷の等価インピーダンスは、ここから送電線と受電側変圧器の直列インピーダンス j0.3 p.u. を除いた 1.0976-j0.17805 p.u. に等しい。事故前の線路電流$\dot{I}$による電源側リアクタンス j1.4 p.u. に生じる電圧降下分を考慮すると、発電機内部電圧の大きさは、

$|\dot{V_1}+j1.4\dot{I}|=\left|\dot{V_1}+j1.4\left(\frac{\dot{V_1}}{\dot{Z_1}}\right)\right|\\ =|\dot{V_1}|\left|1+\frac{j1.4}{\dot{Z_1}}\right|\\ =|1.0×[1.0+j1.4(0.9-j0.1)]| $

と得られる。この大きさは、
　$\sqrt{(1.14^2+1.26^2)}$ ≒ 1.70　→　1.70 p.u.　…（答）

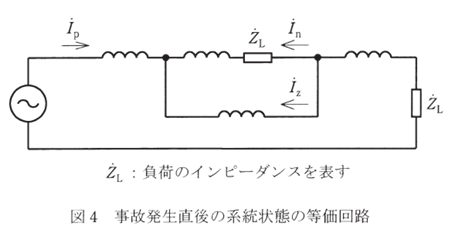
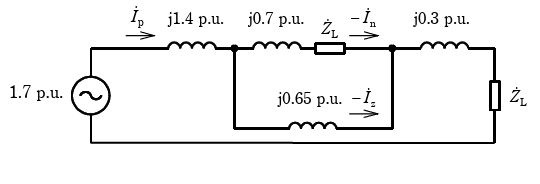
b.　以上をもとに前問で求めた等価回路を、発電機内部電圧を位相の基準とし、インピーダンスをまとめた形で書き直すと次のようになる。
（ただし、$\dot{Z_L}$=1.0976+j0.17805 p.u.）

　上図の$\dot{I}_p$を計算すると、

$ \dot{I}_p=\frac{1.7}{j1.7+1.0976-j0.17805+\frac{(1.0976+j0.52195)j0.65}{(1.0976+j0.52195)+j0.65}} $

　≒ 0.3912 – j0.6062 p.u.　…（答）

c.　また、

　$-\dot{I_n}=\frac{j0.65}{\dot{Z_L}+j1.35}$ = 0.283 335 – j0.070 882 416 p.u.
　$-\dot{I_z}=-\dot{I_p}-(-\dot{I_n})$ = 0.107 865 – j0.535 317 584 p.u.
である。
　以上より、変圧器高圧側母線電圧の対称分電圧は、
正相分が 1.7 – j1.4(0.391 2 -j0.606 2) = 0.851 32 – j0.547 68 p.u.
正相分が j0.4 × (-$\dot{I_n}$) = 0.028 352 966 – j0.113 334 p.u.
また、零相分が j0.2 × (-$\dot{I_z}$) = 0.107 063 516 + j0.021 573 p.u.
　したがって、求める電圧は、これらの和をとって、
　(0.851 32 -j0.547 68)+(0.028 353 +j0.113 33)+(0.107 06 +j0.021 573)
　= 0.986 733 – j0.412 777 p.u.
である。
　求める電圧の大きさは、