電験１種過去問【2012年電力管理 問3】

解答

公式標準解答(※太字は補足)

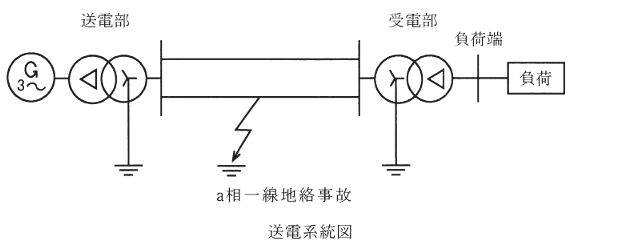
1. 　事故前は負荷端の電圧の大きさが 1.0 [p.u.] で運用されている。このときの発電機の正相リアクタンス背後電圧の大きさ及び送電線の中間地点の電圧の大きさを p.u.値で求めよ。なお、変圧器の巻数比は全て基準状態（p.u.にて 1：1 ）とする。

　負荷は電圧1.0[p.u.]のとき、皮相電力0.5[p.u]で遅れ力率0.9なので、有効電力0.5×0.9=0.45、無効電力は0.5×\(\sqrt{1.0-(0.9)^2}\)=0.2179で与えられる。
このため、負荷端電圧1.0+j0[p.u.]とすると、負荷に流れる電流は0.45-j0.2179[p.u.]で表される。（∵複素電力\(\dot{S}\)=0.45+j0.2179=V×\(\bar{I}\)）
これから、単相表現の送電系統は下図の図となる。

　負荷は\(\frac{1.0+j0}{0.45-j0.2179}\)=1.800+j0.8717[p.u.]で得られる。

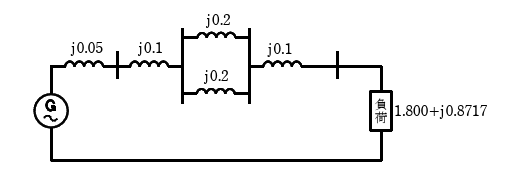
　この回路図より、負荷端子電圧を1.0[p.u]に保つために必要な発電機背後電圧\(\dot{V}_z\)は、
\(\dot{V}_z\)=1.0+j0.35(0.45-j0.2179)=1.0763+j0.1575
よって、|\(\dot{V}_z\)|=1.088[p.u.]
通常運用時は２回線送電線に均等に電流が流れるので、事故点の故障前電圧\(\dot{V}_{f0}\)は、
\(\dot{V}_{f0}\)=1.0+j0.15×(0.45-j0.2179)=1.0327+j0.0675
よって、|\(\dot{V}_{f0}\)|=1.0349[p.u.]　→　1.035[p.u.]

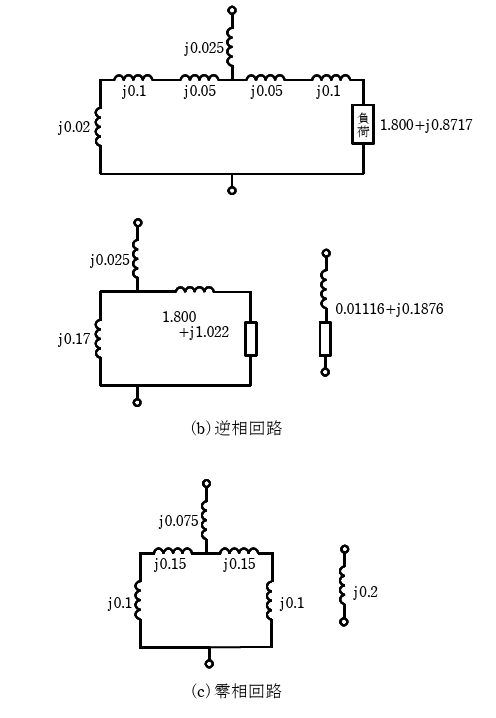
2.　送電線の事故点からみた、対象座標法における、送電系統の正相、逆相、零相回路をそのインピーダンス値を含めて示せ。

　問題の送電系統における、正相、逆相、零相回路は次のように書ける。

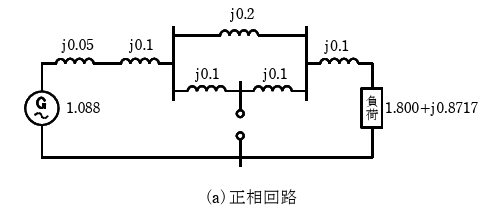
　発電機の正相回路には、正相起電力が含まれる。発電機の逆相起電力は零であるので、逆相リアクタンスのみを考える。変圧器は、送電線と同様に、正相であっても逆相であっても漏れリアクタンスを考える。

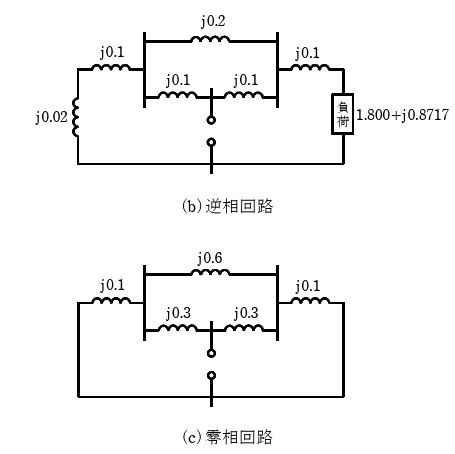
　変圧器の零相回路は、Δ-Y結線で中性点接地の場合、漏れリアクタンスと接地抵抗の3倍（本題では0[p.u.]）でY側が短絡される回路となる。（Δ側は開放回路となる。）

3.　2. で求めた正相、逆相、零相回路を鳳・テブナンの等価回路で表せ。

　正相、逆相、零相回路は次のように簡略化できる。

　正相回路ではまず、下図上部のようにΔ回路(j0.1-j0.1-j0.2)をY回路(j0.025-j0.05-j0.05)にΔ-Y変換する。その後、鳳・テブナンの等価回路の手法を使って、端子間の開放端電圧(正相電圧\(\dot{V}_{f0}\))を計算、電源短絡除去による端子間インピーダンス(正相インピーダンスZ₁)を計算する。

|\(\dot{V}_{f0}\)|は前問 1. で求めているが、検算のため計算してみる。
\(\dot{V}_{f0}\)=(1.0763+j0.1575)×\(\frac{j0.15+(1.8+j0.8717)}{j0.2+j0.15+(1.8+j0.8717)}\)
　=1.032711+j0.067495[p.u.]
|\(\dot{V}_{f0}\)|=1.03491[p.u.]

\(\dot{Z}_1\)=j0.025+\(\frac{j0.2(1.8+j1.0217)}{j0.2+(1.8+j1.0217)}\)=0.01521+j0.214673[p.u.]

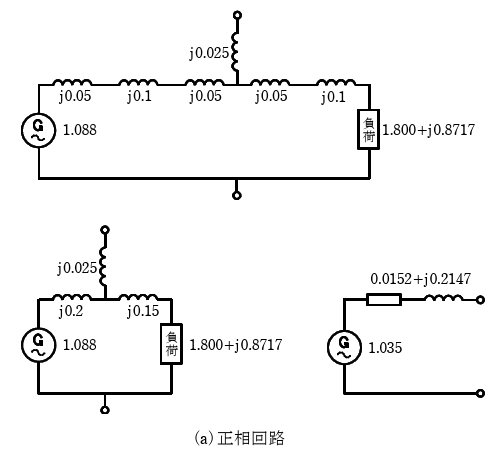
逆相回路・零相回路でも、正相回路と同様にΔ-Y変換を行い、端子間インピーダンスZ₂及びZ₀を計算する。

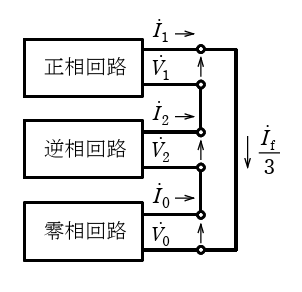
4.　図に示すように、片方の回線の中間地点で a 相一線地絡事故が発生したとき、その状態を示す正相、逆相、零相回路を接続した図をその理由と共に示せ。

a 相での一線地絡事故を考えると、地絡インピーダンスを 0 とするため、地絡点におけるそれぞれの相の電圧と電流は\(\left\{ \begin{array}{l}\dot{V}_a=0\\ \dot{I}_b=\dot{I}_c=0\end{array} \right.\)とおける。
　\(\dot{V}_0,\dot{V}_1,\dot{V}_2\)をそれぞれ零相、正相、逆相電圧、\(\dot{I}_0,\dot{I}_1,\dot{I}_2\)をそれぞれ零相、正相、逆相電流とすると、

\( \begin{bmatrix} \dot{I}_0 \\ \dot{I}_1 \\ \dot{I}_2  \end{bmatrix} =\displaystyle \frac{1}{3} \begin{bmatrix} 1 & 1 & 1 \\ 1 & α & α^2 \\ 1 & α^2 & α \end{bmatrix} \begin{bmatrix} \dot{I}_a \\ 0 \\ 0  \end{bmatrix} \) 　 \( \begin{bmatrix} \dot{V}_a \\ \dot{V}_b \\ \dot{V}_c  \end{bmatrix} = \begin{bmatrix} 1 & 1 & 1 \\ 1 & α^2 & α \\ 1 & α & α^2 \end{bmatrix} \begin{bmatrix} \dot{V}_0 \\ \dot{V}_1 \\ \dot{V}_2 \end{bmatrix} \) 　 \(\displaystyle\left(α=1\angle\frac{2}{3}\pi=-\frac{1}{2}+j\frac{\sqrt3}{2}\right)\)

より、\(\left\{ \begin{array}{l}\dot{V}_a=\dot{V}_0+\dot{V}_1+\dot{V}_2=0\\ \dot{I}_0=\dot{I}_1=\dot{I}_2=\frac{1}{3}\dot{I}_a\end{array} \right.\)を得る。

　対称座標法における、この条件を満たす回路構成は零相、正相、逆相回路を直列に接続した図となる。

5.　a 相一線地絡事故点における地絡電流 [kA] を計算せよ。

　3. 、4. の結果より a 相一線地絡事故の地絡電流\(\dot{I}_{f}\) [kA] は次式で表される。
　\(\dot{I}_{f}=\frac{3×1.035}{(0.0152+0.0112)+j(0.2147+0.1876+0.2)}\)=0.2255-j5.1454 [p.u.]
　よって、|\(\dot{I}_{f}\)|=5.1503 [p.u.] となる。
　基準電流\({I}_{S}\)は\({I}_{S}=\frac{1000}{\sqrt3×500}\)=1.1547 [kA] で与えられるので、
地絡電流|\(\dot{I}_{f}\)|は
　1.155 × 5.150 = 5.9483　→　5.95 [kA]

解説

　対称座標法を用いての一線地絡故障計算に関する問題です。対象座標法を用いた一線地絡故障のお手本の問題となります。一種受験者は対称座標法の解法を理解しておく必要があります。計算が複雑となるので、他選択問題とのバランスを考慮しなければなりません。

難易度５（★★★★☆）

追加学習は対称座標法による故障計算、送電の学習帳で