電験2種過去問【2019年理論 問7】
【電子回路】界磁中の電子の運動(サイクロトロン共鳴)《空所問題》
次の文章は、磁界中の電子の運動に関する記述である。文中の\(\fbox{空所欄}\)に当てはまる最も適切なものを解答群の中から選べ。
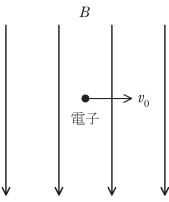
図のように、磁束密度B(>0)の一様な磁界に直角に速度\(v_0(>0)\)で電子(質量m、電荷-e、e>0)が運動している。このとき電子は磁界からローレンツ力を受ける。その力の向きは電子の進行方向に直角で\(\fbox{(1)}\)の方向であり、その大きさは\(F=\fbox{(2)}\)である。電子はこの力を向心力として半径rの円運動をすることから、 \(r= \fbox{(3)}\)となる。また、電子が回転する角周波数は\(\omega =\fbox{(4)}\)である。ここに角周波数が\(\omega\)と等しい振動電界を外部から印加することにより、電子を効率よく加速したり減速したりすることができる。電子が加速された場合には、電子の速度\(v_0\)が増大することから、円運動の半径は増大する。このとき、電子の円運動の角周波数\(\omega\)の大きさは\(\fbox{(5)}\)。この現象はサイクロトロン共鳴と呼ばれ、高密度プラズマの生成や、固体の有効質量の測定などに応用されている。
[問7の解答群]
\(\small{\begin{array}{ccc}
(イ)&\displaystyle\frac{eB}{m}&(ロ)&増大する&(ハ)&\displaystyle\frac{mv_0^2}{eB}\\
(ニ)&減少する&(ホ)&\displaystyle\frac{mv_0}{eB}&(ヘ)&\displaystyle\frac{eB}{v_0}\\
(ト)&\displaystyle\frac{m}{eB}&(チ)&ev_0^2B&(リ)&紙面表から裏へ\\
(ヌ)&紙面裏から表へ&(ル)&\displaystyle\frac{ev_0B}{m}&(ヲ)&変わらない\\
(ワ)&ev_0B&(カ)&磁界Bと逆向き&(ヨ)&\displaystyle\frac{eB}{2\pi m}\\
\end{array}}\)


ディスカッション
コメント一覧
まだ、コメントがありません