解答
(3)
解説
電界E[V/m]中に置かれた点電荷Q[C]にかかる力F[N]は、Q>0のとき力の向きは電界の向きと同じとなり、
F=QE[N] …(1)
仕事W[J]は、F[N]の力でd[m]移動したとすると
W=Fd[J] …(2)
式(1)、(2)より
W=QEd[J]
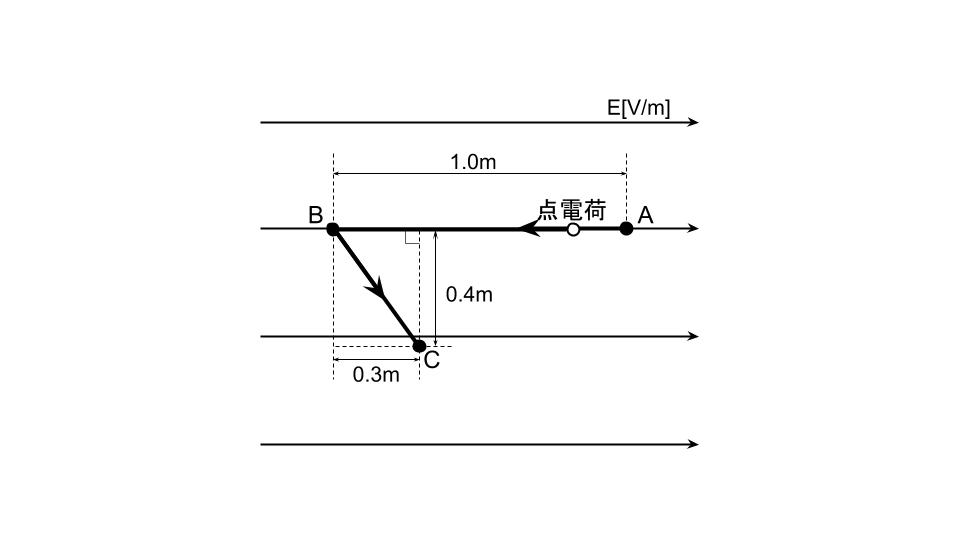
上記のように、電荷2[C]にかかる、静電力F(画面の右方向)に対して、反対方向(画面の左方向)移動した距離のみが、与えられた外力の仕事となる。
点電荷2[C]を外力にによって移動させるには、電界E[V/m]による静電力F[N](静電力の方向は、電界の方向と同一)と反対方向にF[N]と同等以上の大きさの外力を加える必要がある。この時、必要な最低限の外力をFAB[N]とすると、
FAB≒F=QE=2E[N]
従って、外力による仕事W[J]は、静電力Fに反するFABの外力で正反対方向に移動した距離d=0.7mであるので、
W=FABd=2E×0.7=1.4E=14[J]
すなわち、E=10[V/m]となる。
点Aの電位に対する点Bの電位VBA[V]の値は、点Aと点Bの距離d=1mであるので
VBA=E×d=10[V]
【外力による仕事が分かりにくいひとのために】
外力による仕事は「力×移動量」となる。点Aから点Bまでの1.0mの移動に、電界と反対方向に、外力による仕事が必要となる。
しかし、この後に点Bから点Cまで移動する際に、電界と同じ方向に静電力によって0.3m移動するが、これはマイナスの外力による仕事が与えられたと考える。結果として与えられた外力の仕事は、電界と反対方向に0.7m移動した分のみとなる。
電界と垂直方向(画面下方向)に0.4m移動した分の外力による仕事はどうか。垂直方向には何の力もかかっておらず、下方向に移動するには下方向の外力が必要となる。下方向に外力を加え0.2m移動したのち、C点で電荷が止まるためには、上方向に同様の外力を与えれば0.2m移動したのち電荷は静止する。つまり、電界と垂直方向の外力による仕事はプラスマイナスゼロとなり、何の仕事も与えられていないと考えることができる。


ディスカッション
コメント一覧
まだ、コメントがありません