解答
公式標準解答(※太字は補足)
1. 短絡前の母線sの電圧を\(\dot{E}_{s1}\)[p.u.]、同母線から系統を見た正相インピーダンスを\(\dot{Z}_{s1}\)[p.u.]とするとき、母線sにおけるbc相2相短絡故障時の正相短絡電流\(\dot{I}_{s1}\)[p.u.]の式を求めよ。
母線sにおけるbc相短絡故障時の abc 変数の電圧・電流制約式は下記。
\(\left. \begin{array}{l}
\dot{V}_{sb}=\dot{V}_{sc}\\
\dot{I}_{sa}=0\\
\dot{I}_{sb}+\dot{I}_{sc}=0
\end{array} \right\}\)
これを 012 変数で表すと、
\(\left. \begin{array}{l}
\dot{V}_{s0}=0\\
\dot{V}_{s1}=\dot{V}_{s2}\\
\dot{I}_{s1}+\dot{I}_{s2}=0
\end{array} \right\}\)
したがって、零相成分は出現しない。一方、母線sにおける正・逆相の故障基本式は下記。
\(\left\{ \begin{array}{l}
\dot{V}_{s1}=\dot{E}_{s}-\dot{Z}_{s1}・\dot{I}_{s1}\\
\dot{V}_{s2}=-\dot{Z}_{s2}・\dot{I}_{s2}
\end{array} \right.\)
以上から正相分変数を取り出して、
\(\displaystyle \dot{I}_{s1}=\frac{\dot{E}_{s}}{\dot{Z}_{s1}+\dot{Z}_{s2}}\\
\displaystyle =\frac{\dot{E}_{s}}{2\dot{Z}_{s1}}\)…(答) (∵題意より\(\dot{Z}_{s2}=\dot{Z}_{s1}\))
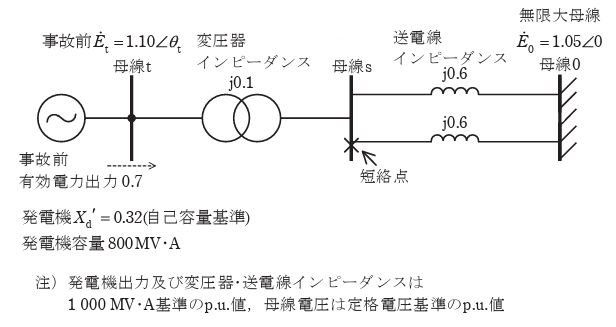
2. 図の値を用いて sinθt の値を求め、これを用いて短絡前の母線sの電圧の絶対値\(\dot{E}_{s}\)[p.u.]を求めよ。
母線tの電圧\(\dot{E}_{t}\)を求め、この\(\dot{E}_{t}\)と\(\dot{E}_{0}\)の関係から短絡前の母線sの電圧\(\dot{E}_{s}\)を求める。
まず、母線tの sinθt は、母線 t-0 間のリアクタンスを Xt0 とするとき、
\(\displaystyle P=\frac{E_tE_0sinθ_t}{X_{t0}}\)から
\(\displaystyle 0.7=\frac{1.10×1.05sinθ_t}{0.1+\frac{0.6}{2}}\)
これから sinθt = 0.242 42 → 0.242 …(答)
これから cosθt = \(\sqrt{1-sinθ_t^2}\) = 0.970 17 (∵題意より |θ|<\(\frac{π}{2}\))
すなわち、母線tの短絡前の電圧\(\dot{E}_{t}\)は、
\(\dot{E}_{t}\)=1.10(0.970 17+j0.242 42)=1.067 2+j0.266 66
上から、短絡前母線sの\(\dot{E}_{s}\)は次式で求まる。
\(\dot{E}_{s}\)=0.75\(\dot{E}_{t}\)+0.25\(\dot{E}_{0}\)
=0.75×(1.0672+j0.266 66)+0.25×(1.05+j0)
=1.062 9+j0.2
【注:\(\dot{E}_{s}\)値は、他の手順でも導出できる。例えば、母線 t-0 間の電流\(\displaystyle \dot{I}_{0}=\frac{\dot{E}_{t}-\dot{E}_{0}}{j0.4}\)を求め、\(\dot{E}_{s}=\dot{E}_{0}+j0.3\dot{I}_{t0}\)からも導出できる。(これら2式をまとめて表現すると上式になる)】
上記\(\dot{E}_{s}\)の絶対値を採って、
\(\dot{E}_{t}\)= 1.081 5 → 1.08 …(答)
3. 図の値を用いて、母線sから系統を見た正相インピーダンス\(\dot{Z}_{s1}\)の値[p.u.]を求めよ。
母線sから右側のインピーダンス\(\dot{Z}_{1R}\)と左側インピーダンス\(\dot{Z}_{1L}\)を計算し、これらの並列和として\(\dot{Z}_{s1}\)を求める。
まず、\(\dot{Z}_{1R}\)は、
\(\dot{Z}_{1R}=\displaystyle\frac{j0.6}{2}\)=j0.3
また、\(\dot{Z}_{1L}\)は、
\(\dot{Z}_{1L}=j0.1+j\displaystyle\frac{0.32}{0.8}\)=j0.5
これらから\(\dot{Z}_{s1}\)は、
\(\dot{Z}_{s1}=\displaystyle\frac{\dot{Z}_{1R}×\dot{Z}_{1L}}{\dot{Z}_{1R}+\dot{Z}_{1L}}\)= j0.187 5 → j0.188 …(答)
4. 上記bc相2相短絡故障時の正相短絡電流の絶対値\(\dot{I}_{s1}\)[p.u.]、及びこのときの母線sの正相電圧の絶対値\(\dot{V}_{s1}\)[p.u.]を求めよ。
2相短絡故障時の正相短絡電流の絶対値\(\dot{I}_{s1}\)は、小問1. の式から、
\(\dot{I}_{s1}=\displaystyle \left| \frac{\dot{E}_s}{2\dot{Z}_{s1}}\right|=\frac{1.081 5}{2×0.187 5}\)=2.884 → 2.88 …(答)
また、このときの母線sの正相電圧\(\dot{V}_{s1}\)は、小問1. の式から、
\(\dot{V}_{s1}=\dot{E}_{s}-\dot{Z}_{s1}・\displaystyle\frac{\dot{E}_{s}}{2\dot{Z}_{s1}}=\frac{\dot{E}_{s}}{2}\)
これから、
\(\dot{V}_{s1}=\displaystyle\frac{1.081 5}{2}\)=0.540 75 → 0.541 …(答)
【注:上記\(\dot{V}_{s1}\)値は、他の手順でも導出できる。単純には\(\dot{V}_{s1}=\dot{E}_{s}-\dot{Z}_{s1}・\dot{I}_{s1}\)の右辺に直接各値を代入する方法もあるし、また\(\dot{V}_{s1}=\dot{Z}_{s1}・\dot{I}_{s1}\)(正相電圧=逆相電圧,正相電流+逆相電流=0の条件を利用)からも求めることもできる。】
解説
管理人が、1種受験時に歯がたたず、涙を飲んだ問題です。対称座標法を用いての2相短絡故障計算に関する問題です。対象座標法を用いて2相短絡故障の条件付けから関係式の導出の全てを行う必要があり、さらに実務的な回路からの故障時正相電圧を解答することが求めれられています。対象座標法を理解できていれば及第点を狙える問題です。一種受験者はこのレベルの対称座標法の解法は理解しておきたいところです。こちらに対称座標法による故障計算をまとめています。
難易度4(★★★★☆)

ディスカッション
コメント一覧
まだ、コメントがありません