電験3種過去問【2021年理論 問9】
2022年4月24日
【電気回路】RLC共振回路の動作《正誤問題》
実効値V[V]、角周波数ω[rad/s]の交流電圧源、R[Ω]の抵抗R、インダクタンスL[H]のコイルL、静電容量C[F]のコンデンサCからなる共振回路に関する記述として、正しいものと誤りのものの組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
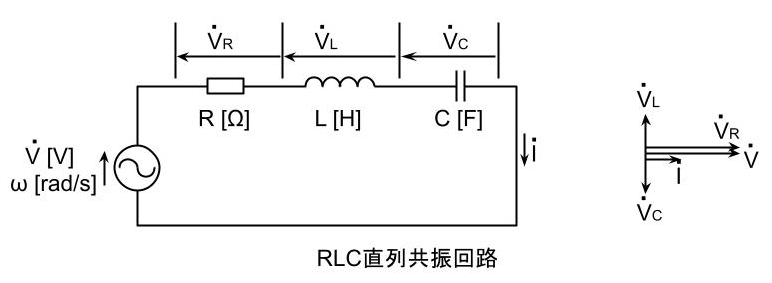
- RLC直列回路の共振状態において、LとCの端子間電圧の大きさはともに0である。
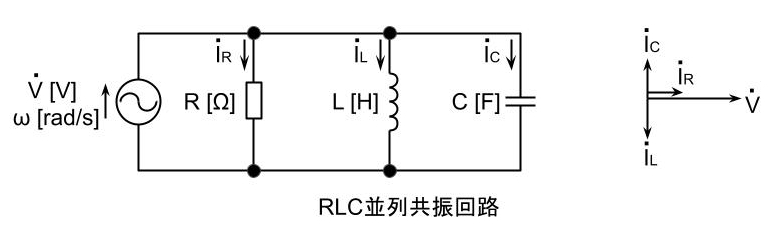
- RLC並列回路の共振状態において、LとCに電流は流れない。
- RLC直列回路の共振状態において交流電圧源を流れる電流は、RLC並列回路の共振状態において交流電圧源を流れる電流と等しい。
| (a) | (b) | (c) | |
| (1) | 誤り | 誤り | 正しい |
| (2) | 誤り | 正しい | 誤り |
| (3) | 正しい | 誤り | 誤り |
| (4) | 誤り | 誤り | 誤り |
| (5) | 正しい | 正しい | 正しい |
(1) RLC直列回路及びRLC並列回路の共振条件は、LによるインピーダンスZL[Ω]とCによるインピーダンスZC[Ω]が等しいことである。つまり、 \(\displaystyle Z_L=Z_C\) すなわち、 \(\displaystyle ωL=\frac{1}{ωC}\) \(\displaystyle ω=\frac{1}{\sqrt{LC}}\) \(\displaystyle 2\pi f=\frac{1}{\sqrt{LC}}\) \(\displaystyle f=\frac{1}{2\pi\sqrt{LC}}\) 回路の電源周波数\(\displaystyle f=\frac{1}{2\pi\sqrt{LC}}\)が成り立つとき、RLC回路は共振状態となる。 (a)上図のRLC直列回路では、回路に流れる電流\(\displaystyle \dot{I}\)を基準に考えると、 抵抗に掛かる電圧\(\displaystyle \dot{V_R}\)は、\(\displaystyle \dot{I}\)と同位相となる。 インダクタンスに掛かる電圧\(\displaystyle \dot{V_L}\)は、\(\displaystyle \dot{I}\)に対して90°進み位相となる。 コンデンサに掛かる電圧\(\displaystyle \dot{V_C}\)は、\(\displaystyle \dot{I}\)に対して90°遅れ位相となる。 ここで、\(\displaystyle \dot{V_L}\)の大きさは、 \(\displaystyle V_L=Z_L I\) また、\(\displaystyle \dot{V_C}\)の大きさは、 \(\displaystyle V_C=Z_C I\) 共振条件より、\(\displaystyle Z_L=Z_C\)であるので、 \(\displaystyle V_L=V_C\) 電源電圧\(\displaystyle \dot{V}\)は、各RLCに印加される電圧のベクトル和となるので \(\displaystyle \dot{V}=\dot{V_R}+\dot{V_L}+\dot{V_C}=\dot{V_R}\) (\(\displaystyle \dot{V_L}\)と\(\displaystyle \dot{V_C}\)は逆向きで同じ大きさなので打ち消しあう) 電流Iの大きさは、 \(\displaystyle I=\frac{V_R}{R}=\frac{V}{R}\text{[A]}\) 以上より LとCのそれぞれの端子間電圧は、 \(\displaystyle V_L=Z_L I\)と\(\displaystyle V_C=Z_C I\)が生じていて、ともに0ではない。 LとCの端子間電圧を一括して測定すると、 \(\displaystyle \dot{V_L}+\dot{V_C}=0\)となる。 (b)上図のRLC並列回路では、回路にかかる電圧\(\displaystyle \dot{V}\)を基準に考えると、 抵抗に流れる電流\(\displaystyle \dot{I_R}\)は、\(\displaystyle \dot{V}\)と同位相となる。 インダクタンスに流れる電流\(\displaystyle \dot{I_L}\)は、\(\displaystyle \dot{V}\)に対して90°遅れ位相となる。 コンデンサに流れる電流\(\displaystyle \dot{I_C}\)は、\(\displaystyle \dot{V}\)に対して90°進み位相となる。 ここで、\(\displaystyle \dot{I_L}\)の大きさは、 \(\displaystyle I_L=\frac{V}{Z_L}\) また、\(\displaystyle \dot{I_C}\)の大きさは、 \(\displaystyle I_C=\frac{V}{Z_C}\) 共振条件より、\(\displaystyle Z_L=Z_C\)であるので、 \(\displaystyle I_L=I_C\) 電源電流\(\displaystyle \dot{I}\)は、各RLCに流れる電流のベクトル和となるので \(\displaystyle \dot{I}=\dot{I_R}+\dot{I_L}+\dot{I_C}=\dot{I_R}\) (\(\displaystyle \dot{I_L}\)と\(\displaystyle \dot{I_C}\)は逆向きで同じ大きさなので打ち消しあう) 電流Iの大きさは、 \(\displaystyle I=I_R=\frac{V}{R}\text{[A]}\) 以上より LとCのそれぞれには、 \(\displaystyle I_L=\frac{V}{Z_L}\)と\(\displaystyle I_C=\frac{V}{Z_C}\)の電流が流れる。 LとCに流れる電流を合わせて測定すると、 \(\displaystyle \dot{I_L}+\dot{I_C}=0\)となる。 (c)上記解説(a)及び(b)より、直列RLC共振回路と並列RLC共振回路の電源に流れる電流Iは、ともに \(\displaystyle I=\frac{V}{R}\text{[A]}\) となり、等しい。解答
解説
関連記事
電験3種過去問【2015年法規 問5】
【電気設備技術基準の解釈】変圧器に施す接地工事に関する記述《空所問題》 次の文 ...
電験3種過去問【2011年機械 問6】
【変圧器】交流電気機器の損失に関する記述《正誤問題》 次の文章は、交流電気機器 ...
電験3種過去問【2012年電力 問11】
【配電】地中電線路の無負荷充電容量計算《計算問題》 電圧 6.6 ,周波数 5 ...
電験2種過去問【2021年理論 問4】
【電気回路】角周波数による合成リアクタンスの変化《空所問題》 次の文章は、正弦 ...
電験2種過去問【2021年理論 問5】
【電気回路】LCR直列回路の過渡現象《空所問題》 次の文章は、電気回路の過渡現 ...


ディスカッション
コメント一覧
まだ、コメントがありません