電験3種過去問【2021年理論 問8】
【電気回路】正弦波交流電流の瞬時値《正誤問題》
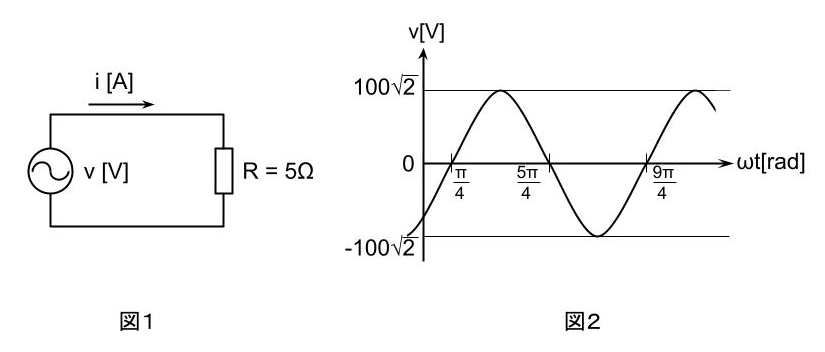
図1の回路において、図2のような波形の正弦波交流電圧v[V]を抵抗5Ωに加えたとき、回路を流れる電流の瞬時値i[A]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。ただし、電流の周波数を50Hz、角周波数をω[rad/s]、時間をt[s]とする。
(1) \(\displaystyle 20\sqrt2 \sin\left(50\pi t-\frac{\pi}{4}\right)\)
(2) \(\displaystyle 20\sin\left(50\pi t+\frac{\pi}{4}\right)\)
(3) \(\displaystyle 20\sin\left(100\pi t-\frac{\pi}{4}\right)\)
(4) \(\displaystyle 20\sqrt2 \sin\left(100\pi t+\frac{\pi}{4}\right)\)
(5) \(\displaystyle 20\sqrt2 \sin\left(100\pi t-\frac{\pi}{4}\right)\)


ディスカッション
コメント一覧
まだ、コメントがありません