解答
(2)
解説
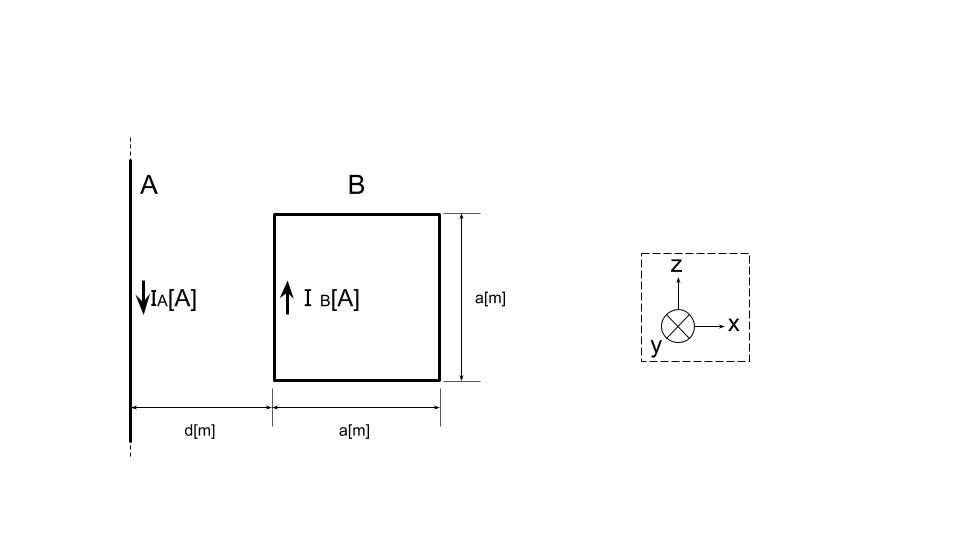
磁束密度B[Wb/m2]の磁界を垂直に横切る、長さL[m]の導線に、I[A]の電流が流れているとき、導線には
F=BLI[N] …(1)
の力が働く。力の方向はフレミングの左手の法則に従う。
いまAの無限長直線状導体に電流IA[A]が流れているとき、この導体からr[m]離れた点に発生する磁束密度B[Wb/m2]は
B=μ0IA/(2πa) …(2)
となる。磁束の向きはアンペアの右ねじの法則に従い、xz平面上の導体Bに対しては、画面の奥から手前の方向(-y方向)となる。
(2)式からわかるように、導体Aによって発生する磁束密度は、導体Aから離れるにつれて弱くなる。いま、導体Bのx方向の2辺に関しては、導体Aにより生じる磁束密度は一様に弱まっていくため、各辺に発生する力は互いに打ち消しあう。このため導体Bのz方向の2辺に生じる力のみ考えればよい。
導体Aからd[m]離れた、導体Bのz方向の一辺に働く力をFd[N]とすると、導体Aによりd[m]離れた点に生じる磁束密度Bd[Wb/m2]は(2)式よりBd=μ0IA/(2πd)である。(1)式より、
Fd=BdaIB=μ0IAIBa/(2πd)[N] …(3)
一方、導体Aからa+d[m]離れた、導体Bのz方向の一辺に働く力をFa+d[N]とすると、導体Aによりa+d[m]離れた点に生じる磁束密度Ba+d[Wb/m2]は(2)式よりBa+d=μ0IA/{2π(a+d)}である。(1)式より、
Fa+d=Ba+daIB=μ0IAIBa/{2π(a+d)}[N] …(4)
フレミングの左手の法則により、式(3)の力はx方向に働き、式(4)の力は-x方向に働く。式(3)と式(4)を比べると、分子は等しく分母は(4)が大きいため、(3)>(4)でありx方向に力が働く。x方向の力を正とすると導体Bに働く力FB[N]は
FB=μ0IAIBa/(2πd)-μ0IAIBa/{2π(a+d)}
={μ0IAIBa(a+d)-μ0IAIBad}/{2πd(a+d)}
={μ0IAIBa(a+d-d)}/{2πd(a+d)}
=μ0IAIBa2/{2πd(a+d)}


ディスカッション
コメント一覧
まだ、コメントがありません