電験２種過去問【2021年機械 問6】

解答

(１)：（ヲ）
(２)：（ホ）
(３)：（チ）
(４)：（ワ）
(５)：（ヌ）

解説

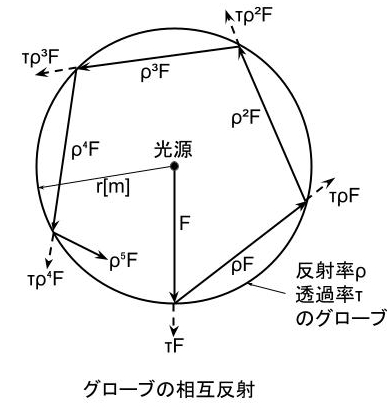
　乳白ガラスでできたグローブ(球体、半径r[m])がある。グローブの中心には点光源(全光束F_p[lm])が置かれている。グローブの内側と外側の表面はともに均等拡散面である。点光源を発してグローブ内側表面に入射した光は、一部は反射され、残りは乳白ガラスに進入する。なお、乳白ガラスの厚みは無視でき、乳白ガラスの反射率及び透過率はρおよびτとする。
　また、グローブの内側表面で反射された光はグローブ内を進行して内側表面のどこかに再び入射し、そこで一部は反射され、残りは乳白ガラスに進入する。光はこのような過程をグローブ内で繰り返すが、グローブの内側表面で反射された光が点光源に吸収されることはないものとする。なお、円周率はπとする。
　以上の諸量を用いて、グローブから外側に放射される全光束F_Sは$\displaystyle \frac{τF_p}{1-ρ}$[lm]で表される。またF_Sを用いて、グローブの光度Iは$\displaystyle \frac{F_s}{4\pi}$[cd]、光束発散度Mは$\displaystyle \frac{F_s}{4\pi r^2}$[lm/m²]で表される。
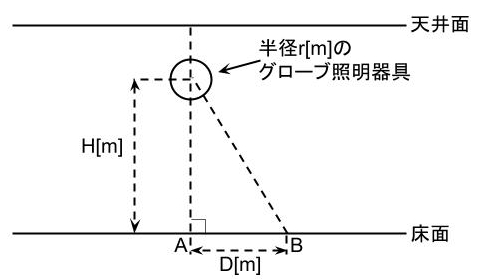
　次に、図に示すように、このグローブ照明器具を部屋の天井面からつるし、部屋の照明を行った。グローブ中心直下の床面上の位置A点からグローブ中心までの高さはH[m]で、H≫rである。また、A点から床面上のB点までの距離はD[m]である。なお、この部屋にはグローブ照明器具以外に光源はなく、天井、床、壁など、周囲からの反射光や入射光の影響はないものとする。
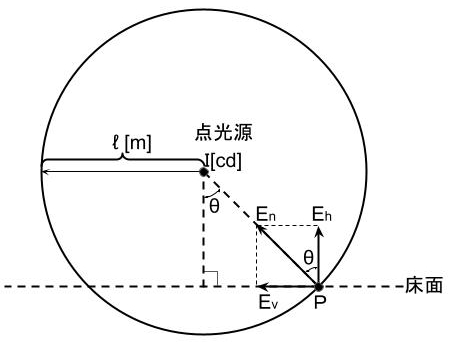
　B点における水平面照度E_hはグローブの光度Iを用いて$\displaystyle \frac{HI}{\left(H^2+D^2\right)^{\frac{3}{2}}}$[lx]で表される。また、B点からグローブの中心を見たときの輝度Lは光束発散度Mを用いて$\displaystyle \frac{M}{\pi}$[cd/m²]となる。

グローブ内の相互反射

下図にように、光源の光束をF[lm]、グローブの反射率をρ、透過率をτとする。

透過光束$\displaystyle F_τ$[lm]は

$\displaystyle F_τ=τF+τρF+τρ^2F+τρ^3F+…$

$\displaystyle =τF(1+ρ+ρ^2+ρ^3+…)$

$\displaystyle =τF\frac{1}{1-ρ}$　∵等比数列$\displaystyle \sum_{i=0}^\infty x_i=\frac{1}{1-x}　(|x|<1)$

で与えられる。

問題では、グローブの中心には全光束F_p[lm]の点光源が置かれているので、グローブから外側に放射される全光束F_Sは

$\displaystyle \frac{τF_p}{1-ρ}$[lm]

光度

光源から出てある方向の立体角Δωに放射される光束をΔFとするとき

光度Iは下式で定義される。

$\displaystyle I=\frac{ΔF}{Δω}\text{[cd]}$

ここで、全球の立体角ω＝4π[sr](ステラジアン)である。

問題では、グローブから全球方向（ω＝4π[sr]）に放射される光束F_Sを用いて光度Iを表すと、

$\displaystyle \frac{F_s}{4\pi}$[cd]

光束発散度

光束発散度Mは光源から発散される光束$\displaystyle F_0$[lm]について、光源の全表面上$\displaystyle A_0$[m²]から拡散する密度で表す。

$\displaystyle M=\frac{F_0}{A_0}\text{[rlx]}$

問題では、グローブの全表面積（A₀＝4πr²[m²]）から拡散される光束F_Sを用いて、光束発散度Mは

$\displaystyle \frac{F_s}{4\pi r^2}$[lm/m²]で表される。

水平面照度

光度の定義$\displaystyle I=\frac{ΔF}{Δω}\text{[cd]}$より、

光度I[cd]の点光源からは

$\displaystyle F=4\pi I\text{[lm]}$

の光束が全空間(ω=4π)に均等に発散している。

下図のように、点光源を中心とした半径l[m]の球を考えると、点光源からのすべての光束は球表面に到達する。このため球の表面の照度Ｅ[lx]は

$\displaystyle E=\frac{F}{S}=\frac{4\pi I}{4\pi l^2}=\frac{I}{l^2}\text{[lx]}$

ここで表される照度Ｅはその点から球の中心（点光源）へ向かう方向の照度で法線照度$\displaystyle E_n$と呼ぶ。

法線照度　　$\displaystyle E_n=\frac{I}{l^2}\text{[lx]}$

水平面照度　$\displaystyle E_h=\frac{I}{l^2}cos\theta\text{[lx]}$

鉛直面照度　$\displaystyle E_v=\frac{I}{l^2}sin\theta\text{[lx]}$

 

問題では、B点における水平面照度E_hはグローブの光度Iを用いて

$\displaystyle E_h=\frac{I}{(\sqrt{H^2+D^2})^2}cos\theta\text{[lx]}$

$\displaystyle cos\theta =\frac{H}{\sqrt{H^2+D^2}}$であるので、

$\displaystyle E_h=\frac{I}{(\sqrt{H^2+D^2})^2}\frac{H}{\sqrt{H^2+D^2}}$

$\displaystyle =\frac{HI}{\left(H^2+D^2\right)^{\frac{3}{2}}}$[lx]で表される。

輝度

輝度L[cd/m²]は、光源を観測点から見た時、観測点を通過する単位面積S（観測者から見て垂直な平面上に投影した正射影面積）当たりの光度Iで定義される。

$\displaystyle L=\frac{I}{S}$[cd/m²]

問題では、B点からグローブの中心を見たときの輝度Lは

$\displaystyle L=\frac{I}{S}=\frac{\frac{F_s}{4\pi}}{\pi r^2}=\frac{F_s}{\pi \times4 \pi r^2}$[cd/m²]

光束発散度$\displaystyle M=\frac{F_s}{4\pi r^2}$[lm/m²]を用いて

$\displaystyle L=\frac{M}{\pi}$[cd/m²]となる。