電験１種過去問【2021年機械制御問4】

2021年12月1日2024年9月8日

【自動制御】古典制御におけるフィードバック制御系の解析《計算問題》

　図に示すフィードバック制御系について、次の問に答えよ。

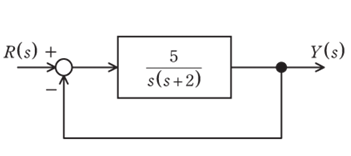
（１）目標値R(s)から制御量Y(s)までの閉ループ伝達関数W(s)を求めよ。
（２）閉ループ伝達関数W(s)の固有角周波数ω_nと減衰係数 ζ を求めよ。
（３）目標値R(s)をt=0で単位ステップで変化させたときの制御量の時間応答y(t)を求めよ。
　必要に応じて、ラプラス変換の複素領域における推移定理である
　ℒ[e^-atx(t)]=X(s+a)を使ってよい。
（４）小問(3)の時間応答y(t)は減衰振動となる。y(t)を時間微分し、t>0における一つ目の極値が最大値であることを使って、時間応答y(t)が最大となる時間t_pを求めよ。
（５）小問(3)の時間応答y(t)の最大値y(t_p)を求めよ。

解答と解説はこちら